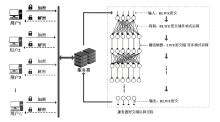
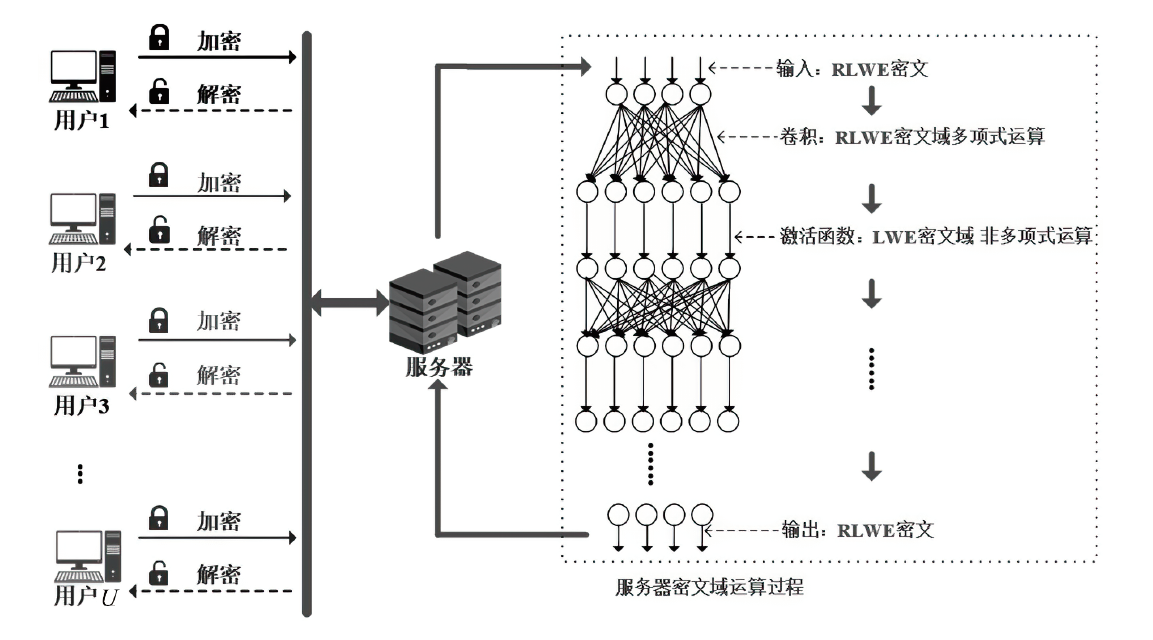
| [1] |
DOWLIN N, GILAD-BACHRACH R, LAINE K, et al. CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy[C]// ACM. Proceedings of the 33rd International Conference on Machine Learning. New York: ACM, 2016: 201-210.
|
| [2] |
BRUTZKUS A, ELISHA O, GILAD-BACHRACH R. Low Latency Privacy Preserving Inference[C]// ACM. Proceedings of the 36th International Conference on Machine Learning. New York: ACM, 2019: 1295-1304.
|
| [3] |
LOU Qian, JIANG Lei. SHE: A Fast and Accurate Deep Neural Network for Encrypted Data[C]// ACM. Proceedings of the 33rd International Conference on Neural Information Processing Systems. New York: ACM, 2019: 10035-10043.
|
| [4] |
BOURSE F, MINELLI M, MINIHOLD M, et al. Fast Homomorphic Evaluation of Deep Discretized Neural Networks[C]// Springer. 38th Annual International Cryptology Conference. Berlin:Springer, 2018: 483-512.
|
| [5] |
BRAKERSKI Z, GENTRY C, VAIKUNTANATHAN V. (Leveled) Fully Homomorphic Encryption Without Bootstrapping[C]// ACM. Proceedings of the 3rd Innovations in Theoretical Computer Science Conference. New York: ACM, 2014: 309-325.
|
| [6] |
FAN Junfeng, VERCAUTEREN F. Somewhat Practical Fully Homomorphic Encryption[EB/OL]. (2012-01-16)[2022-12-01]. http://eprint.iacr.org/2012/144.
|
| [7] |
CHEON J H, KIM A, KIM M, et al. Homomorphic Encryption for Arithmetic of Approximate Numbers[C]// Springer. International Conference on the Theory and Applications of Cryptology and Information Security. Berlin:Springer, 2017: 409-437.
|
| [8] |
DUCAS L, MICCIANCIO D. FHEW: Bootstrapping Homomorphic Encryption in Less than a Second[C]// Springer. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin:Springer, 2015: 617-640.
|
| [9] |
CHILLOTTI I, NICOLAS G, MARIYA G, et al. TFHE Fast Fully Homomorphic Encryption over the Torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.
doi: 10.1007/s00145-019-09319-x
|
| [10] |
CHEON J H, KIM D, KIM D. Efficient Homomorphic Comparison Methods with Optimal Complexity[C]// Springer. International Conference on the Theory and Application of Cryptology and Information Security. Berlin:Springer, 2020: 221-256.
|
| [11] |
CHEON J, KIM D, KIM D, et al. Numerical Method for Comparison on Homomorphically Encrypted Numbers[C]// Springer. International Conference on the Theory and Application of Cryptology and Information Security. Berlin:Springer, 2019: 415-445.
|
| [12] |
MICCIANCIO D, POLYAKOV Y S. Bootstrapping in FHEW-Like Cryptosystems[EB/OL]. (2021-09-19)[2022-12-01]. https://eprint.iacr.org/2020/086.
|
| [13] |
BOURA C, GAMA N, GEORGIEVA M, et al. CHIMERA: Combining Ring-LWE-Based Fully Homomorphic Encryption Schemes[J]. Journal of mathematical cryptology, 2020, 14(1): 316-338.
doi: 10.1515/jmc-2019-0026
URL
|
| [14] |
LU Wenjie, HUANG Zhicong, HONG Cheng, et al. PEGASUS: Bridging Polynomial and Non-Polynomial Evaluations in Homomorphic Encryption[C]// IEEE. 2021 IEEE Symposium on Security and Privacy. New York: IEEE, 2021: 1057-1073.
|
| [15] |
REGEV O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography[C]// ACM. Proceedings of the 37th Annual ACM Symposium on Theory of Computing. New York: ACM, 2005: 84-93.
|
| [16] |
LYUBASHEVSKY V, PEIKERT C, REGEV O. On Ideal Lattices and Learning with Errors over Rings[C]// Springer. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin:Springer, 2010: 1-23.
|
| [17] |
GENTRY C, SAHAI A, WATERS B. Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based[C]// Springer. Annual Cryptology Conference. Berlin:Springer, 2013: 75-92.
|
| [18] |
HAN K, HHAN M, CHEON J H. Improved Homomorphic Discrete Fourier Transforms and FHE Bootstrapping[J]. IEEE Access, 2019, 7: 57361-57370.
doi: 10.1109/ACCESS.2019.2913850
|
| [19] |
CHEN Hao, DAI Wei, KIM M, et al. Efficient Homomorphic Conversion Between (Ring) LWE Ciphertexts[C]// Springer. Applied Cryptography and Network Security 19th International Conference. Berlin:Springer, 2021: 460-479.
|
| [20] |
HAN K, KI D. Better Bootstrapping for Approximate Homomorphic Encryption[C]// Springer. Cryptographers’ Track at the RSA Conference. Berlin:Springer, 2020: 364-390.
|
| [21] |
Microsoft. Microsoft SEAL[EB/OL]. (2018-12-03)[2022-12-01]. https://github.com/microsoft/SEAL.
|
 ), HAN Yiliang2, WANG Xu’an2
), HAN Yiliang2, WANG Xu’an2