Netinfo Security ›› 2021, Vol. 21 ›› Issue (4): 62-72.doi: 10.3969/j.issn.1671-1122.2021.04.007
Previous Articles Next Articles
Network Attack Path Analysis Method Based on Vulnerability Dynamic Availability
ZHANG Kai1,2,3, LIU Jingju1,3( )
)
- 1. College of Electronic Engineering, National University of Defense Technology, Hefei 230037, China
2. Jiuquan Satellite Launch Center, Jiuquan 732750, China
3. Anhui Province Key Laboratory of Cyberspace Security Situation Awareness and Evaluation, Hefei 230037, China
-
Received:2020-08-11Online:2021-04-10Published:2021-05-14 -
Contact:LIU Jingju E-mail:jingjul@aliyun.com
CLC Number:
Cite this article
ZHANG Kai, LIU Jingju. Network Attack Path Analysis Method Based on Vulnerability Dynamic Availability[J]. Netinfo Security, 2021, 21(4): 62-72.
share this article
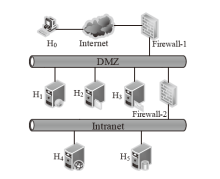
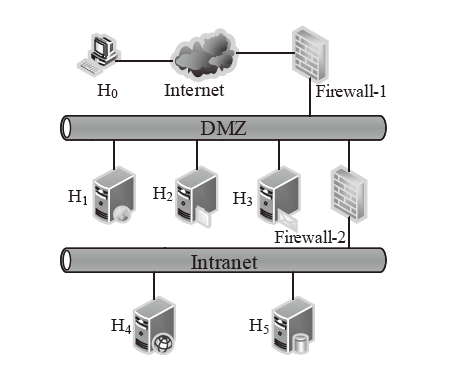
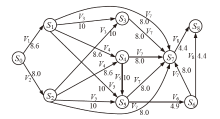
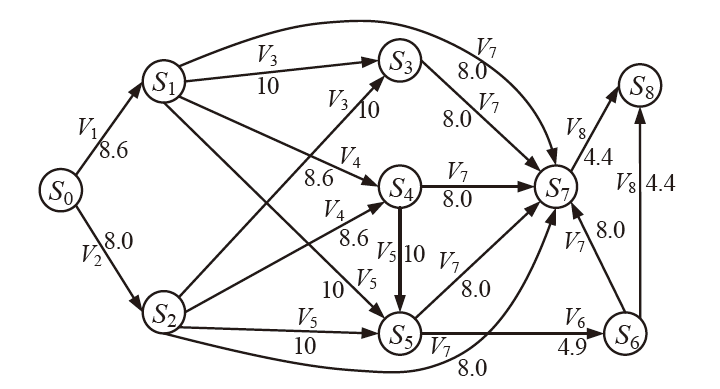
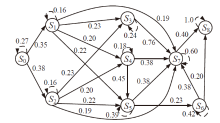
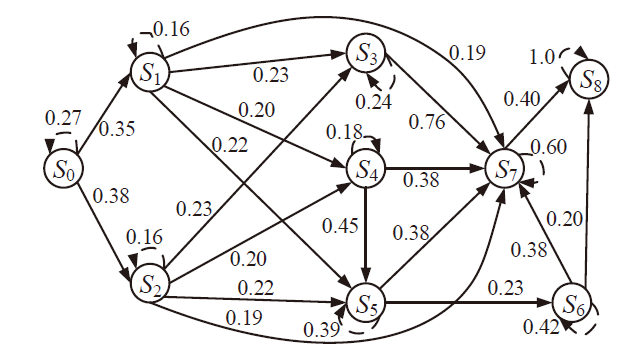
| 主机 | 服务/应用 | 漏洞 | 编号 | 可利用性得分 | 披露时间 |
|---|---|---|---|---|---|
| H1 | openSSh | CVE-2019-6111 | V1 | 8.6 | 2019.1.31 |
| Apache ATS 6.2.2 | CVE-2018-8004 | V2 | 8.0 | 2018.8.29 | |
| H2 | TFTP Server | CVE-2018-8476 | V3 | 10 | 2018.11.13 |
| H3 | Oracle E-Business Suite 12.1.1 | CVE-2019-2491 | V4 | 8.6 | 2019.1.17 |
| H4 | IBM Security Key Lifecycle Manager 3.0 | CVE-2018-1751 | V5 | 10 | 2019.1.23 |
| Windows Server 2008 R2 | CVE-2018-8345 | V6 | 4.9 | 2018.8.15 | |
| H5 | MySQL Server 8.0.12 | CVE-2018-3286 | V7 | 8.0 | 2018.10.16 |
| CVE-2019-2503 | V8 | 4.4 | 2019.1.16 |
| [1] | LIU Xinran, LI Baisong, CHANG Anqi, et al. The Current Network Security Situation and Emergency Network Response[J]. Strategic Study of CAE, 2016,18(6):83-88. |
| 刘欣然, 李柏松, 常安琪, 等. 当前网络安全形势与应急响应[J]. 中国工程科学, 2016,18(6):83-88. | |
| [2] | YANG Junnan, ZHANG Hongqi, ZHANG Chuanfu, et al. Intrusion Path Prediction Based on Incomplete Information Multi-stage Game[J]. Application Research of Computers, 2019,36(2):519-524. |
| 杨峻楠, 张红旗, 张传富, 等. 基于不完全信息多阶段博弈的入侵路径预测[J]. 计算机应用研究, 2019,36(2):519-524. | |
| [3] | KORDY B, PIÈTRE-CAMBACÉDÈS L, SCHWEITZER P. DAG-based Attack and Defense Modeling: Don't Miss the Forest for the Attack Trees(Review)[J]. Computer Science Review, 2014,13(11):1-38. |
| [4] | YANG Yingjie, LENG Qiang, CHANG Dexian, et al. Research on Network Dynamic Threat Analysis Technology Based on Attribute Attack Graph[J]. Journal of Electronics & Information Technology, 2019,41(8):1838-1846. |
| 杨英杰, 冷强, 常德显, 等. 基于属性攻击图的网络动态威胁分析技术研究[J]. 电子与信息学报, 2019,41(8):1838-1846. | |
| [5] | WANG Hui, RU Xinxin, DAI Tianwang, et al. Attack Profit Path Prediction Algorithm Based on NAPG Model[J]. Journal of Jilin University(Science Edition), 2019,37(5):1169-1178. |
| 王辉, 茹鑫鑫, 戴田旺, 等. 基于NAPG模型的攻击增益路径预测算法[J]. 吉林大学学报(理学版), 2019,37(5):1169-1178. | |
| [6] | HU Hao, LIU Yuling, ZHANG Hongqi, et al. Route Prediction Method for Network Intrusion Using Absorbing Markov Chain[J]. Journal of Computer Research and Development, 2018,55(4):831-845. |
| 胡浩, 刘玉岭, 张红旗, 等. 基于吸收Markov链的网络入侵路径预测方法[J]. 计算机研究与发展, 2018,55(4):831-845. | |
| [7] | WANG Fan. Research on Network Security Risk Assessment Method Based on Bayesian Attack Graph[D]. Xi’an: Northwest University, 2018. |
| 王帆. 基于贝叶斯攻击图的网络安全风险评估方法研究[D]. 西安:西北大学, 2018. | |
| [8] | LIU Yu, MAN Hong. Network Vulnerability Assessment Using Bayesian Networks[EB/OL]. https://spie.org/Publications/Proceedings/Paper/10.1117/12.604240, 2020-05-31. |
| [9] |
POOLSAPPASIT N, DEWRI R, RAY I. Dynamic Security Risk Management Using Bayesian Attack Graphs[J]. IEEE Transactions on Dependable and Secure Computing, 2012,9(1):61-74.
doi: 10.1109/TDSC.2011.34 URL |
| [10] | FANG Yan, YIN Xiaochuan, LI Jingzhi. Research of Quantitative Network Security Assessment Based on Bayesian-attack Graphs[J]. Application Research of Computers, 2013,30(9):2763-2766. |
| 方研, 殷肖川, 李景志. 基于贝叶斯攻击图的网络安全量化评估研究[J]. 计算机应用研究, 2013,30(9):2763-2766. | |
| [11] | MA Chunguang, WANG Chenghong, ZHANG Donghong, et al. A Dynamic Network Risk Assessment Model Based on Attacker’s Inclination[J]. Journal of Computer Research and Development, 2015,58(9):2056-2068. |
| 马春光, 汪诚弘, 张东红, 等. 一种基于攻击意愿分析的网络风险动态评估模型[J]. 计算机研究与发展, 2015,58(9):2056-2068. | |
| [12] | WANG Yang, WU Jianying, HUANG Jinlei, et al. Network Intrusion Intention Recognition Method Based on Bayesian Attack Graph[J]. Computer Engineering and Applications, 2019,55(22):73-79. |
| 王洋, 吴建英, 黄金垒, 等. 基于贝叶斯攻击图的网络入侵意图识别方法[J]. 计算机工程与应用, 2019,55(22):73-79. | |
| [13] | WANG Shuo, TANG Guangming, KOU Guang, et al. Attack Path Prediction Method Based on Causal Knowledge Net[J]. Journal on Communications, 2016,37(10):188-198. |
| 王硕, 汤光明, 寇广, 等. 基于因果知识网络的攻击路径预测方法[J]. 通信学报, 2016,37(10):188-198. | |
| [14] | YUSUF S E, GE M, HONG J B, et al. Evaluating the Effectiveness of Security Metrics for Dynamic Networks[C]// IEEE. 2017 IEEE Trustcom/BigDataSE/ICESS, August 1-4, 2017, Sydney, NSW, Australia. NJ: IEEE, 2017: 277-284. |
| [15] | YUSUF S E, GE M, HONG J B, et al. Security Modelling and Analysis of Dynamic Enterprise Networks[C]// IEEE. 2016 IEEE International Conference on Computer & Information Technology, December 8-10, 2016, Nadi, Fiji. NJ: IEEE, 2016: 249-256. |
| [16] | ABRAHAM S, NAIR S. Cyber Security Analytics: A Stochastic Model for Security Quantification Using Absorbing Markov Chains[J]. Journal of Communications, 2014,9(12):899-907. |
| [17] | ABRAHAM S, NAIR S. A Predictive Framework for Cyber Security Analytics using Attack Graphs[J]. International Journal of Computer Networks & Communications, 2015,7(1):1-17. |
| [18] |
FENG Pinghui, LIAN Yifeng, DAI Yingxia, et al. A Vulnerability Model of Distributed Systems Based on Reliability Theory[J]. Journal of Software, 2006,17(7):1633-1640.
doi: 10.1360/jos171633 URL |
| 冯萍慧, 连一峰, 戴英侠, 等. 基于可靠性理论的分布式系统脆弱性模型[J]. 软件学报, 2006,17(7):1633-1640. | |
| [19] | WANG Xiujuan, SUN Bo, LIAO Yanwen, et al. Computer Network Vulnerability Assessment Based on Bayesian Attribute Network[J]. Journal of Beijing University of Posts and Telecommunications, 2015,38(4):110-116. |
| 王秀娟, 孙博, 廖彦文, 等. 贝叶斯属性攻击图网络脆弱性评估[J]. 北京邮电大学学报, 2015,38(4):110-116. | |
| [20] | GRINSTEAD C M, SNELL J L. Introduction to Probability[M]. Rhodel Island: American Mathematical Soc, 2012. |
| [21] | HU Hao, YE Runguo, ZHANG Hongqi, et al. Vulnerability Life Cycle Oriented Security Risk Metric Method[J]. Journal of Software, 2018,29(5):1213-1229. |
| 胡浩, 叶润国, 张红旗, 等. 面向漏洞生命周期的安全风险度量方法[J]. 软件学报. 2018,29(5):1213-1229. | |
| [22] | FREI S. Security Econometrics: The Dynamics of (in) Security[M]. Charlton: BookSurge Publishing, 2009. |
| [23] | YOUSEFI M, MTETWA N, ZHANG Yan, et al. A Novel Approach for Analysis of Attack Graph[C]// IEEE. 2017 IEEE International Conference on Intelligence and Security Informatics, July 22-24, 2017, Beijing, China. NJ: IEEE, 2017: 7-12. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||