基于TD-ERCS序列的S盒非线性度优化算法

doi:10.3969/j.issn.1671-1122.2021.01.002

摘要/Abstract

摘要：

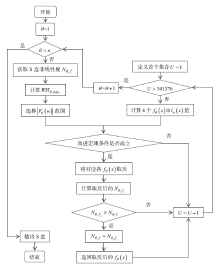
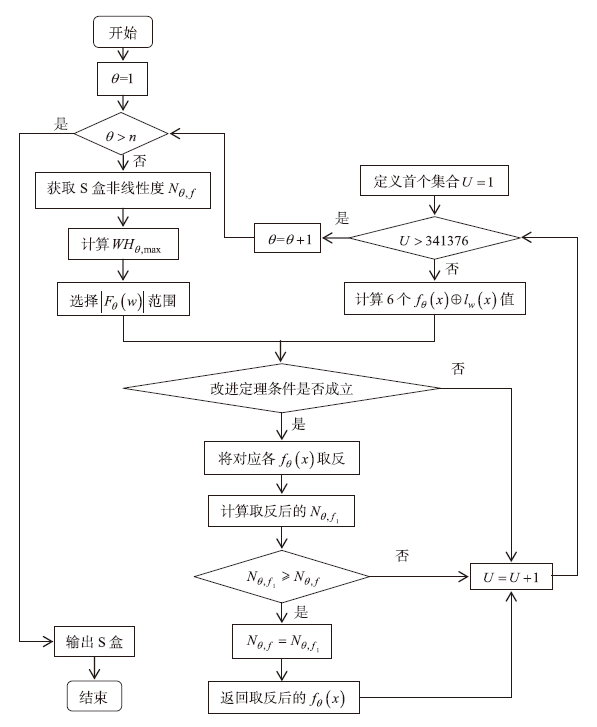
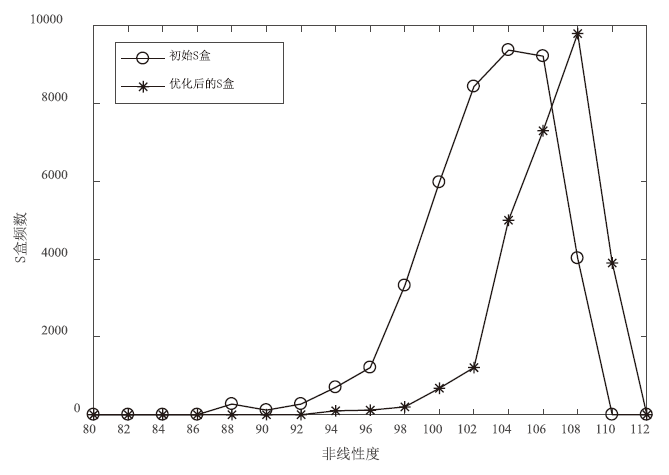
针对基于混沌系统生成的S盒存在非线性度较低等问题,文章针对基于切延迟椭圆反射腔映射系统（TD-ERCS）生成S盒的方法,首先证明了生成的S盒具有双射性,在此基础上,设计了一种改进的爬山算法,通过动态缩小布尔函数Walsh-Hadamard变换（WHT）的选取范围,将满足条件的6个布尔值进行取反运算,有效提升了双射S盒非线性度。理论和实验仿真分析表明,采用优化算法生成的S盒性能得到了有效提升,在算法效率、非线性度、严格雪崩准则和差分逼近概率等方面具备更好的性能。

关键词: TD-ERCS, 双射性, 非线性度

Abstract:

Aiming at the problems that the S-boxes generated by chaotic systems have lower nonlinearity, in this paper, aims at the method of generating S-boxes based on a mapping system of tangent-delay ellipse reflecting cavity(TD-ERCS), proves the S-boxes have bijection firstly. On this basis, an improved hill-climbing algorithm is designed. By dynamically reducing the selection ranges of Walsh-Hadamard transform(WHT) of Boolean functions, and inverting six Boolean values satisfying the conditions, the nonlinearities of bijective S-boxes are improved. Theoretical and experimental simulation analysis shows that, the performance of S-boxes generated by optimization algorithm is improved effectively, and has better performance in algorithm efficiency, nonlinearity, strict avalanche criterion and differential approximation probability.

Key words: TD-ERCS, bijection, nonlinearity

中图分类号:

TP309

张雪锋, 卫凯莉, 姜文. 基于TD-ERCS序列的S盒非线性度优化算法[J]. 信息网络安全, 2021, 21(1): 10-18.

ZHANG Xuefeng, WEI Kaili, JIANG Wen. The Nonlinearity Optimization Algorithm of S-box Based on TD-ERCS Sequence[J]. Netinfo Security, 2021, 21(1): 10-18.

图/表 14

表1

图1

图2

表2

表3

表4

表5

表6

表7

表8

表9

表10

表11

表12

参考文献 34

[1]	AYESHA R, MAJID K. Construction of New S-boxes Based on Triangle Groups and Its Applications in Copyright Protection[J]. Multimedia Tools and Applications, 2019,78(6):15527-15544. doi: 10.1007/s11042-018-6953-x URL
[2]	SELCUK K, SEVDENUR B. Results on Symmetric S-boxes Constructed by Concatenation of RSSBs[J]. Cryptography and Communications, 2019,11(7):641-660.
[3]	IMRAN S, QAISER M, ABDUL R. Construction of New S-box Using Action of Quotient of the Modular Group for Multimedia Security[J]. Security and Communication Networks, 2019,2019(11):1-13.
[4]	FIRAT A, FATIH Ö. A Novel Method for Performance Improvement of Chaos Based Substitution Boxes[J]. Symmetry, 2020,12(4):1-13.
[5]	ZHU Honghong, TONG Xiaojun, WANG Zhu, et al. A Novel Method of Dynamic S-box Design Based on Combined Chaotic Map and Fitness Function[J]. Multimedia Tools and Applications, 2020,79(5):12329-12347.
[6]	HUSSAM A A, MOHAMAD F Z, MUSHEER A. A Novel Efficient Substitution-box Design Based on Firefly Algorithm and Discrete Chaotic Map[J]. Neural Computing and Applications, 2019,31(11):7201-7210.
[7]	FATIH Ö, AHMET B Ö. A Method for Designing Strong S-Boxes Based on Chaotic Lorenz System[J]. Physics Letters A, 2010,374(36):3733-3738.
[8]	DRAGAN L. A Novel Method of S-box Design Based on Discrete Chaotic Map[J]. Nonlinear Dynamics, 2017,87(3):2407-2413.
[9]	AKRAM B, AHMED A A E. A Simple Yet Efficient S-box Method Based on Chaotic Sine Map[J]. Optik, 2017,130(2):1438-1444.
[10]	FATIH Ö. Construction of Robust Substitution Boxes Based on Chaotic Systems[J]. Neural Computing and Applications, 2019,31(8):3317-3326. doi: 10.1007/s00521-017-3287-y URL
[11]	KHAWAJA M A, MAJID K. Application Based Construction and Optimization of Substitution Boxes Over 2D Mixed Chaotic Maps[J]. International Journal of Theoretical Physics, 2019,58(9):3091-3117.
[12]	ARSLAN S. A New Algorithm for the Construction of Substitution Box by Using Chaotic Map[J]. The European Physical Journal Plus, 2020,135(9):1-13. doi: 10.1140/epjp/s13360-019-00059-2 URL
[13]	SHENG Liyuan, SUN Kehui, LI Chuanbing. Study on Discrete Chaotic System of Elliptic Reflection Cavity Based on Tangent Delay and Its Performance[J]. Acta Physica Sinica, 2004,53(9):2871-2876. doi: 10.7498/aps.53.2871 URL
	盛利元, 孙克辉, 李传兵. 基于切延迟的椭圆反射腔离散混沌系统及其性能研究[J]. 物理学报, 2004,53(9):2871-2876. doi: 10.7498/aps.53.2871 URL
[14]	ZHANG Linhua, DENG Shaojiang. S-box Construction of Tangent Delay Elliptic Reflection Cavity Mapping System[J]. Journal of Chongqing University, 2009,32(10):1226-1230.
	张林华, 邓绍江. 切延迟椭圆反射腔映射系统的S盒构造[J]. 重庆大学学报, 2009,32(10):1226-1230.
[15]	IQTADAR H, TARIQ S, MUHAMMAD A G, et al. A Novel Method for Designing Nonlinear Component for Block Cipher Based on TD-ERCS Chaotic Sequence[J]. Nonlinear Dynamics, 2013,73(7):633-637. doi: 10.1007/s11071-013-0816-9 URL
[16]	ALI H A, IQTADAR H, MUHAMMAD A G. A Novel Design for the Construction of Safe S-boxes Based on TDERC Sequence[J]. Alexandria Engineering Journal, 2015,54(1):65-69. doi: 10.1016/j.aej.2015.01.003 URL
[17]	WEN Qiaoyan, YANG Yixian. Construction of Boolean Functions with High Nonlinearity[J]. Acta Electronica Sinica, 1997,27(7):108-112.
	温巧燕, 杨义先. 高非线性度布尔函数的构造[J]. 电子学报, 1997,27(7):108-112.
[18]	YANG Tingting. Design of Multi-output Elastic Boolean Functions with High Nonlinearity[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2018.
	杨婷婷. 具有高非线性度的多输出弹性布尔函数的设计[D]. 西安:西安电子科技大学, 2018.
[19]	WANG Yong, ZHANG Zhiqiang, ZHANG Leyu, et al. A Genetic Algorithm for Constructing Bijective Substitution Boxes with High Nonlinearity[J]. Information Sciences, 2020,523(6):152-166.
[20]	KIM K. Construction of DES-like S-Boxes Based on Boolean Functions Satisfying the SAC[EB/OL]. https://doi.org/10.1007/3-540-57332-1_5, 2020-07-12.
[21]	MUHAMMAD A K, VARUN J. A Novel Design of Chaos Based S-Box Using Difference Distribution Table (CD S-Box)[J]. Communications in Computer and Information Science, 2014,42(3):223-230.
[22]	MUHAMMAD A K, ASIM A, VARUN J, et al. A Chaos-based Substitution Box (S-Box) Design with Improved Differential Approximation Probability(DP)[J]. Iranian Journal of Science and Technology Transactions of Electrical Engineering, 2018,42(2):219-238.
[23]	WILLIAM M. How to Improve the Nonlinearity of Bijective S-boxes[J]. Lecture Notes in Computer Science, 1998,38(7):181-192.
[24]	GAO Sheng, MA Wenping, GUO Na, et al. A New Algorithm for Improving the Nonlinearity of S-box[J]. Journal of Xi’an University of Electronic Science and Technology, 2010,37(6):1017-1021.
	高胜, 马文平, 郭娜, 等. 一种提高S盒非线性度的新算法[J]. 西安电子科技大学学报, 2010,37(6):1017-1021.
[25]	YU Yizhou, OU Haiwen. Two Methods to Improve the Nonlinearity of Bijective S-boxes and the Comparison[J]. China New Communication, 2007,9(3):36-39.
	于亦舟, 欧海文. 两种提高双射S盒非线性度的方法及其比较[J]. 中国新通信, 2007,9(3):36-39.
[26]	QIN Guanjie, MA Jianshe, CHENG Xuemin. Method of Improving S-box Nonlinearity Based on Combined Hill Climbing Algorithm[J]. Computer Applications, 2015,35(8):2195-2198.
	覃冠杰, 马建设, 程雪岷. 基于组合式爬山算法提高S盒非线性度的方法[J]. 计算机应用, 2015,35(8):2195-2198. doi: 10.11772/j.issn.1001-9081.2015.08.2195 URL
[27]	LEI Peng. Research on Chaotic S-box Construction and Encryption Algorithm[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2015.
	雷鹏. 基于混沌的S盒构造及其加密算法研究[D]. 重庆:重庆邮电大学, 2015.
[28]	WANG Yong, LEI Peng. A Method for Constructing Bijective S-Box with High Nonlinearity Based on Chaos and Optimization[J]. International Journal of Bifurcation and Chaos, 2015,25(10):1-15.
[29]	PIEPRZYK J, FINKELSTEIN G. Towards Effective Nonlinear Cryptosystem Design[J]. IEEE Proceedings Computers and Digital Techniques, 1988,135(6):325-335.
[30]	IQTADAR H, TARIQ S. Literature Survey on Nonlinear Components and Chaotic Nonlinear Components of Block Ciphers[J]. Nonlinear Dynamics, 2013,74(12):869-904. doi: 10.1007/s11071-013-1011-8 URL
[31]	JAKIMOSKI G, KOCAREV L. Chaos and Cryptography: Block Encryption Ciphers Based on Chaotic Maps[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001,48(2):163-169. doi: 10.1109/81.904880 URL
[32]	WEBSTER A F, TAVARES S E. On the Design of S-boxes[EB/OL]. https://doi.org/10.1007/3-540-39799-X_41, 2020-07-12.
[33]	BIHAM E, SHAMIR A. Differential Cryptanalysis of DES-like Cryptosystems[J]. Journal of Cryptology, 1991,4(1):63-72.
[34]	MATSUI L. Linear Cryptanalysis Method for DES Cipher[EB/OL]. https://doi.org/10.1007/3-540-48285-7_33, 2020-07-12.

混沌值取值范围	${{\chi }_{{g}/{{{2}^{3}}}\;}}\left( X \right)$取值	d₃(X )取值
$0\le \left\| X \right\|<{1}/{8}\;$	0 0 0 0 0 0 0	0
${1}/{8}\;\le \left\| X \right\|<{2}/{8}\;$	1 0 0 0 0 0 0	1
${2}/{8}\;\le \left\| X \right\|<{3}/{8}\;$	1 1 0 0 0 0 0	0
${3}/{8}\;\le \left\| X \right\|<{4}/{8}\;$	1 1 1 0 0 0 0	1
${4}/{8}\;\le \left\| X \right\|<{5}/{8}\;$	1 1 1 1 0 0 0	0
${5}/{8}\;\le \left\| X \right\|<{6}/{8}\;$	1 1 1 1 1 0 0	1
${6}/{8}\;\le \left\| X \right\|<{7}/{8}\;$	1 1 1 1 1 1 0	0
${7}/{8}\;\le \left\| X \right\|\le 1$	1 1 1 1 1 1 1	1

算法	集合复杂度	非线性度提升上限
三点爬山算法^[24]	16581120$\left( A_{256}^{3} \right)$	3
四点爬山算法^[25,26]	4195023360$\left( A_{256}^{4} \right)$	4
雷鹏提出的算法^[27]	262144$\left( 8C_{128}^{1}\left( C_{128}^{1}+C_{128}^{1} \right) \right)$	2
优化后的S盒算法	2731008$\left( 8C_{128}^{3} \right)$	6

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	195	230	252	255	222	193	2	141	198	26	132	117	61	199	6	10
1	112	184	82	244	170	5	145	73	236	237	93	163	54	121	97	12
2	20	78	226	247	188	233	67	126	164	214	116	25	196	246	18	43
3	95	229	177	189	28	192	32	46	88	106	90	45	21	31	62	72
4	225	115	100	42	108	186	178	234	59	220	200	148	134	65	161	130
5	86	11	165	238	150	50	210	219	51	187	48	181	75	1	190	99
6	153	172	251	80	92	84	212	30	13	221	142	201	152	91	89	71
7	232	47	211	179	135	197	175	182	156	125	129	9	29	41	64	63
8	228	103	127	107	120	171	34	44	105	102	96	57	242	58	85	94
9	70	224	215	208	217	7	14	131	119	144	60	138	37	19	174	40
A	239	69	33	203	206	194	216	39	167	22	111	24	169	76	35	56
B	253	241	87	250	77	159	139	147	151	223	66	101	204	68	23	231
C	136	173	122	243	207	162	0	16	160	191	185	118	79	183	15	3
D	245	218	254	227	104	249	157	166	36	149	158	205	154	53	49	113
E	168	133	137	83	202	4	114	110	140	124	176	248	27	81	55	180
F	143	209	38	240	213	17	123	155	235	52	146	128	98	8	109	74

	0	1	2	3	4	5	6	7
0	0.4688	0.4688	0.5781	0.5156	0.4688	0.4531	0.4844	0.5313
1	0.4219	0.5156	0.5781	0.5000	0.5156	0.5469	0.5000	0.4531
2	0.5156	0.4531	0.5000	0.5000	0.5469	0.5000	0.5156	0.5000
3	0.4375	0.4844	0.5156	0.5000	0.4844	0.4219	0.5469	0.6094
4	0.4531	0.4844	0.3906	0.4531	0.5625	0.5313	0.5313	0.4844
5	0.4688	0.5156	0.4219	0.4844	0.5625	0.5156	0.5313	0.4844
6	0.4823	0.4748	0.4593	0.4593	0.4748	0.4966	0.4672	0.4966
7	0.5000	0.5000	0.4219	0.5781	0.5000	0.5156	0.4688	0.5156

S盒	依赖矩阵
S盒	最大值	最小值	平均值
初始S盒^[16]	0.5938	0.3906	0.4914
本文优化S盒	0.6094	0.3906	0.4956
文献[15]	0.5781	0.4063	0.5050
文献[7]	0.5937	0.4218	0.5048
文献[8]	0.625	0.4219	0.5034
文献[9]	0.5625	0.4375	0.5000
文献[10]	0.6094	0.3909	0.4941