基于辅助熵减的神经常微分方程入侵检测模型

doi:10.3969/j.issn.1671-1122.2022.06.001

信息网络安全 ›› 2022, Vol. 22 ›› Issue (6): 1-8.doi: 10.3969/j.issn.1671-1122.2022.06.001

基于辅助熵减的神经常微分方程入侵检测模型

张兴兰, 付娟娟()

北京工业大学信息学部,北京 100124

收稿日期:2022-02-06 出版日期:2022-06-10 发布日期:2022-06-30
通讯作者: 付娟娟 E-mail:memory1721@163.com
作者简介:张兴兰（1970—）,女,山西,教授,博士,主要研究方向为密码学、信息安全|付娟娟（1997—）,女,河南,硕士研究生,主要研究方向为深度学习和入侵检测
基金资助:
国家自然科学基金(61801008)

Auxiliary Entropy Reduction Based Intrusion Detection Model for Ordinary Differential Equations

ZHANG Xinglan, FU Juanjuan()

Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China

Received:2022-02-06 Online:2022-06-10 Published:2022-06-30
Contact: FU Juanjuan E-mail:memory1721@163.com

摘要/Abstract

摘要：

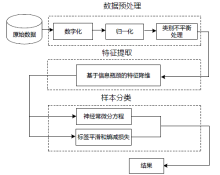
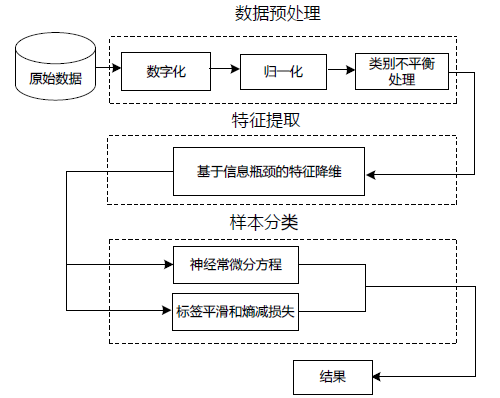
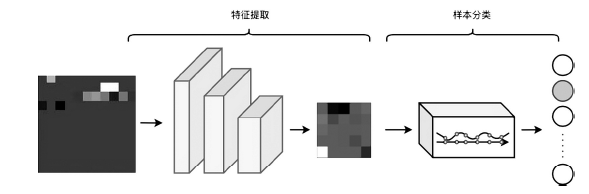
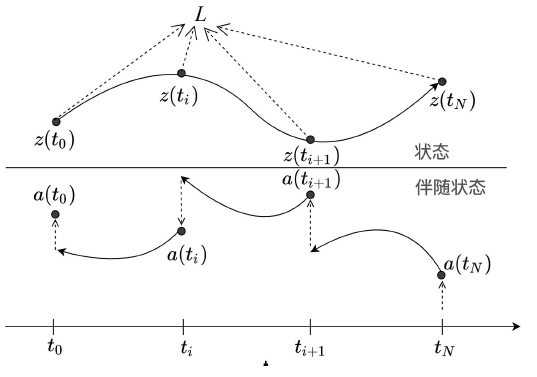
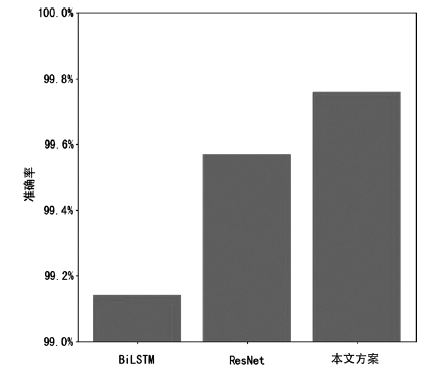
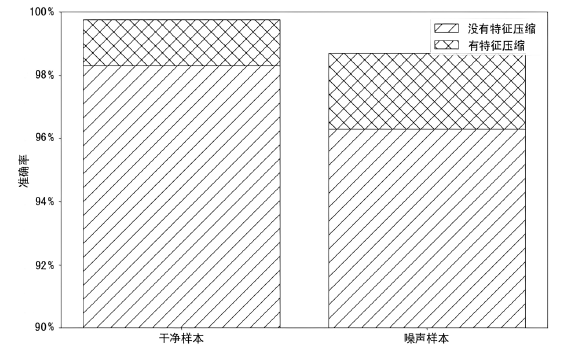
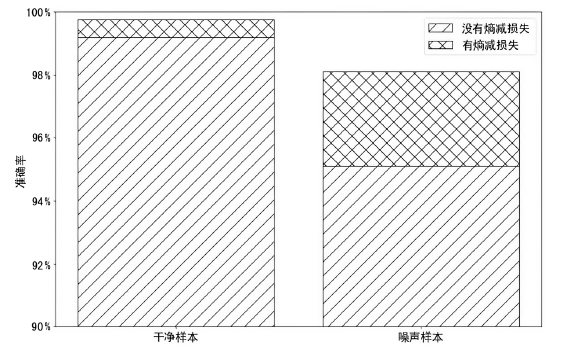
为了提高深度学习模型入侵检测任务的检测效率和分类的准确性,文章提出一种基于辅助熵减的神经常微分方程（E-ODENet）入侵检测模型。该入侵检测模型通过参数常微分方程定义连续的隐藏状态,不需要再分层传播梯度与更新参数,减少了内存的消耗,极大地提高了效率。使用信息瓶颈进行特征降维,提取与分类任务相关的主要信息,同时使用标签平滑和熵减损失来提高模型的泛化能力和准确性。在NSL-KDD数据集上进行训练和测试,测试得到的检测准确率为99.76%,证明该模型优于其他入侵检测模型。

关键词: 入侵检测, 熵减损失, 常微分方程, NSL-KDD

Abstract:

In order to improve the detection efficiency and classification accuracy of the intrusion detection task of deep learning model, this paper proposes an intrusion detection model based on the auxiliary entropy subtraction of the divine ordinary differential equation (E-ODEnet). This intrusion detection model defines continuous hidden states by parametric ordinary differential equations, while does not require further hierarchical propagation of gradients with updated parameters, while reducing memory consumption and greatly improving efficiency. Feature dimensionality reduction is performed using information bottlenecks to extract the main information relevant to the classification task, while label smoothing and entropy reduction loss are used to improve the generalization ability and accuracy of the model. This experiment is trained and tested on the NSL-KDD dataset, and the accuracy rate of the experimental result is 99.76%, which is better than other intrusion detection models.

Key words: intrusion detection, entropy, ODEnet, NSL-KDD

中图分类号:

TP309

张兴兰, 付娟娟. 基于辅助熵减的神经常微分方程入侵检测模型[J]. 信息网络安全, 2022, 22(6): 1-8.

ZHANG Xinglan, FU Juanjuan. Auxiliary Entropy Reduction Based Intrusion Detection Model for Ordinary Differential Equations[J]. Netinfo Security, 2022, 22(6): 1-8.

图/表 11

图1

图2

图3

表1

表2

表3

图4

表4

表5

图5

图6

参考文献 18

[1]	KANG M J, KANG J W, TANG T. Intrusion Detection System Using Deep Neural Network for in-Vehicle Network Security[EB/OL]. [2021-10-28]. https://xueshu.baidu.com/usercenter/paper/show?paperid=345b81696b59762c8cb484998e10a90e.
[2]	LOUKAS G, VUONG T. Cloud-Based Cyber-Physical Intrusion Detection for Vehicles Using Deep Learning[J]. IEEE Access, 2017(6): 3491-3508.
[3]	KIM J, SHIN N, JO S Y, et al. Method of Intrusion Detection Using Deep Neural Network[C]// IEEE. IEEE International Conference on Big Data and Smart Computing. New York: IEEE, 2017: 313-316.
[4]	YIN Chuanlong, ZHU Yuefei. A Deep Learning Approach for Intrusion Detection Using Recurrent Neural Networks[J]. IEEE Access, 2017(5): 21954-21961.
[5]	ZHAO Guangzheng, ZHANG Cuixiao, ZHENG Lijuan. Intrusion Detection Using Deep Belief Network and Probabilistic Neural Network[C]// IEEE. 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC). New York:IEEE, 2017: 639-642.
[6]	WU Kehe, CHEN Zuge, LI Wei. A Novel Intrusion Detection Model for a Massive Network Using Convolutional Neural Networks[J]. IEEE Access, 2018(6): 50850-50859.
[7]	SHONE N, NGOC T N, PHAI V D, et al. A Deep Learning Approach to Network Intrusion Detection[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2018, 2(1): 41-50. doi: 10.1109/TETCI.2017.2772792 URL
[8]	KASONGO S M, SUN Yanxia. A Deep Learning Method with Filter Based Feature Engineering for Wireless Intrusion Detection System[J]. IEEE Access, 2019(7): 38597-38607.
[9]	TANG T A, MHAMDI L. Deep Recurrent Neural Network for Intrusion Detectionin SDN-Based Networks[C]// IEEE. IEEE International Conference on Network Softwarization (NetSoft). New York:IEEE, 2018: 202-206.
[10]	SALAMA M A, EID H F, RAMADAN R A, et al. Hybrid Intelligent Intrusion Detection Scheme[C]// Springer. Online World Conference on Soft Computing in Industrial Applications. Berlin: Springer, 2010: 293-303.
[11]	ZHANG Yong, CHEN Xu, JIN Lei, et al. Network Intrusion Detection: Based on Deep Hierarchical Network and Original Flow Data[J]. IEEE Access, 2019( 7): 37004-37016.
[12]	SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-V4, Inception-ResNet and the Impact of Residual Connections on Learning[J]. Computer Vision and Pattern Recognition, 2017: 4278-4284.
[13]	CHEN R T Q. Neural Ordinary Differential Equations[EB/OL]. [2021-10-26]. https://arxiv.org/abs/1806.07366.
[14]	ALEMI A A. Deep Variational Information Bottleneck[EB/OL]. [2021-10-05]. https://arxiv.org/abs/1612.00410.
[15]	TAVALLAEE M, BAGHERI E, LU W, et al. A Detailed Analysis of the KDD CUP 99 Data Set[C]// IEEE. 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications. New York: IEEE, 2009: 1-6.
[16]	REVATHI S, MALATHI A. A Detailed Analysis on NSL-KDD Dataset Using Various Machine Learning Techniques for Intrusion Detection[J]. International Journal of Engineering Research & Technology, 2013, 2(12): 1848-1853.
[17]	DIRO A A, CHILAMKURTI N. Distributed Attack Detection Scheme Using Deep Learning Approach for Internet of Things[J]. Future Generations Computer Systems, 2017, 82(5): 761-768. doi: 10.1016/j.future.2017.08.043 URL
[18]	GU Jie, LU Shan. An Effective Intrusion Detection Approach Using SVM with Nave Bayes Feature Embedding[EB/OL]. [2021-10-28]. https://xueshu.baidu.com/usercenter/paper/show?paperid=11250ev0nc390vc01y1f0250fu672113.

	数据总数	正常数据	Dos	Probe	R2L	U2R
KDDTrain⁺	125973	67343	45927	11656	995	52
KDDTest⁺	22544	9711	7458	2421	2754	200
KDDTest^-21	11850	2152	4342	2402	2754	200

真实值预测值	异常	正常
异常	TN	FP
正常	FN	TP

模型	ACC	P	R	F1
BiLSTM	99.14%	99.26%	99.14%	99.20%
ResNet	99.57%	99.61%	99.53%	99.57%
本文方案	99.76%	99.73%	99.75%	99.74%

方法	数据集	ACC	P	R	F1
DIRO	NSL-KDD	99.20%	99.02%	99.27%	99.14%
GU	NSL-KDD	99.35%	—	99.24%	—
本文方案	NSL-KDD	99.76%	99.73%	99.75%	99.74%

模型	准确率	时间/s
ResNet	99.57%	0.24
多层感知机（MLP）	99.23%	0.023
本文方案	99.76%	0.098

基于辅助熵减的神经常微分方程入侵检测模型

Auxiliary Entropy Reduction Based Intrusion Detection Model for Ordinary Differential Equations

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 11

参考文献 18

相关文章 15

编辑推荐

Metrics

本文评价

[1]	王浩洋, 李伟, 彭思维, 秦元庆. 一种基于集成学习的列车控制系统入侵检测方法[J]. 信息网络安全, 2022, 22(5): 46-53.
[2]	白宏鹏, 邓东旭, 许光全, 周德祥. 基于联邦学习的入侵检测机制研究[J]. 信息网络安全, 2022, 22(1): 46-54.
[3]	何红艳, 黄国言, 张炳, 贾大苗. 基于极限树特征递归消除和LightGBM的异常检测模型[J]. 信息网络安全, 2022, 22(1): 64-71.
[4]	刘烁, 张兴兰. 基于双重注意力的入侵检测系统[J]. 信息网络安全, 2022, 22(1): 80-86.
[5]	李群, 董佳涵, 关志涛, 王超. 一种基于聚类分类的物联网恶意攻击检测方法[J]. 信息网络安全, 2021, 21(8): 82-90.
[6]	任涛, 金若辰, 罗咏梅. 融合区块链与联邦学习的网络入侵检测算法[J]. 信息网络安全, 2021, 21(7): 27-34.
[7]	杜晔, 王子萌, 黎妹红. 基于优化核极限学习机的工控入侵检测方法[J]. 信息网络安全, 2021, 21(2): 1-9.
[8]	王华忠, 程奇. 基于改进鲸鱼算法的工控系统入侵检测研究[J]. 信息网络安全, 2021, 21(2): 53-60.
[9]	沈也明, 李贝贝, 刘晓洁, 欧阳远凯. 基于主动学习的工业互联网入侵检测研究[J]. 信息网络安全, 2021, 21(1): 80-87.
[10]	李桥, 龙春, 魏金侠, 赵静. 一种基于LMDR和CNN的混合入侵检测模型[J]. 信息网络安全, 2020, 20(9): 117-121.
[11]	徐国天. 网络入侵检测中K近邻高速匹配算法研究[J]. 信息网络安全, 2020, 20(8): 71-80.
[12]	姜楠, 崔耀辉, 王健, 吴晋超. 基于上下文特征的IDS告警日志攻击场景重建方法[J]. 信息网络安全, 2020, 20(7): 1-10.
[13]	张晓宇, 王华忠. 基于改进Border-SMOTE的不平衡数据工业控制系统入侵检测[J]. 信息网络安全, 2020, 20(7): 70-76.
[14]	彭中联, 万巍, 荆涛, 魏金侠. 基于改进CGANs的入侵检测方法研究[J]. 信息网络安全, 2020, 20(5): 47-56.
[15]	王蓉, 马春光, 武朋. 基于联邦学习和卷积神经网络的入侵检测方法[J]. 信息网络安全, 2020, 20(4): 47-54.