对DSA和ECDSA的一种改进格攻击

doi:10.3969/j.issn.1671-1122.2022.02.002

摘要/Abstract

摘要：

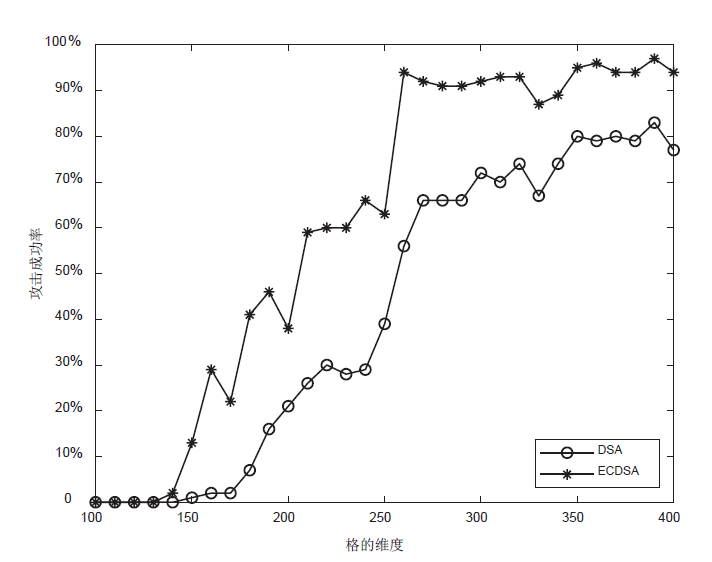
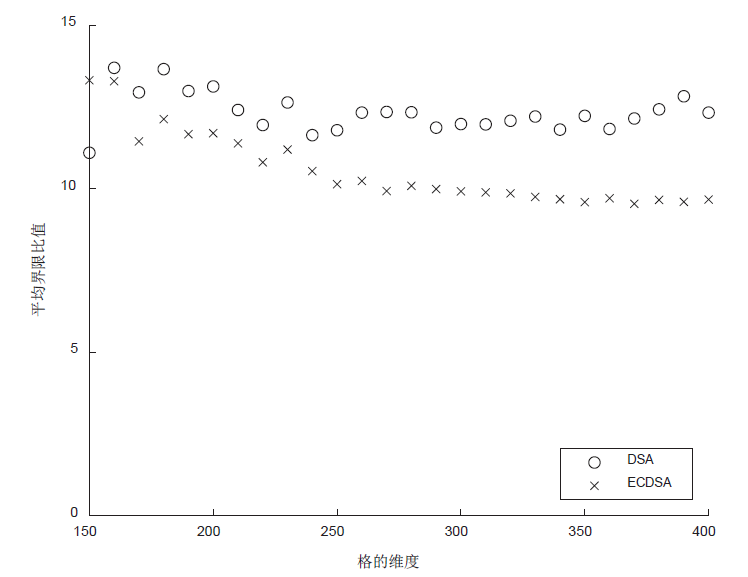
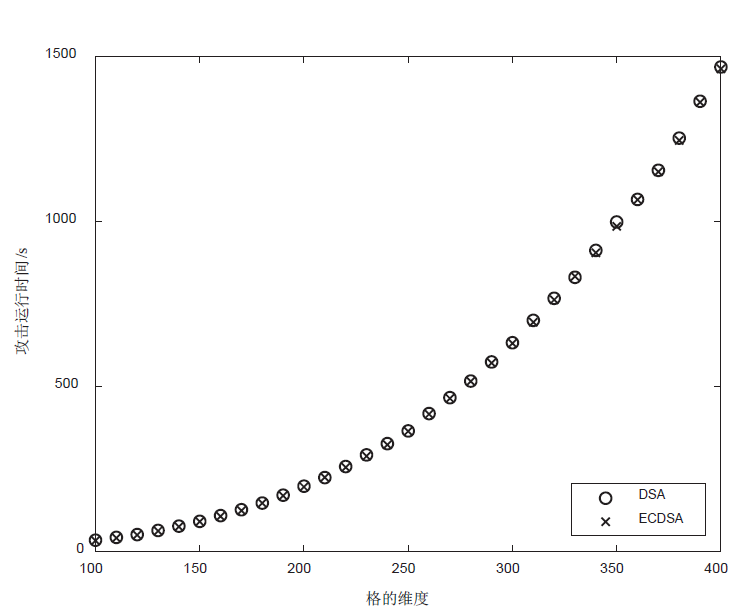
利用格攻击DSA和ECDSA的方法,通过构造同余方程组可以将隐藏数字问题转化为格中最近向量问题,当同余方程组至多有一个解小于给定界限时,可通过求解格中最近向量获取签名私钥。给定界限越大,对解向量的大小要求越宽松,攻击的难度也越低。文章提出一种新的给定界限,其大小是原有界限的6.92倍,显著降低了格攻击的难度。利用从OpenSSL收集到的DSA和ECDSA的签名数据,设计验证新界限的格攻击实验。实验结果表明,新界限对已知解向量元素的要求由最高比特位6位降低到3 位。对于DSA,当格的维度为350时,攻击成功率达80%;对于ECDSA,当格的维度为260时,攻击成功率达97%。通过解向量减去一个基准向量,可将对已知解向量元素的要求降低至1位,从而降低格攻击的难度。

关键词: 格攻击, 隐藏数字问题, 最近向量问题, DSA, ECDSA

Abstract:

The basic idea behind one type of lattice attack to DSA and ECDSA scheme is to construct a system of congruences, and convert the hidden number problem into the nearest vector problem. if one of the solutions of the congruences is below a certain bound, the private key can be found by solving the closest vector. If the bound becomes larger, the size of solution within which the attack is effective can be broadened accordingly, thus reducing the level to construct such congruences. A new bound based on the oretical analysis and calculation was presented. The new bound was 6.92 times larger than the original one, reducing the level to launch an effective lattice attack significantly. This paper designed and implemented experiment to verify this new bound by collecting signatures from OpenSSL. The results show that under the new bound, the lattice attack only require solution vector’s elements’ 3 most significant bits to be known, compared with 6 most significant bits to be known before. For DSA, the success rate is about 80% with a lattice of size 350. For ECDSA, the success rate is about 97% with a lattice of size 260. Furthermore, by subtracting a base vector from the solution vector, the requirement of known bits can be reduced to just one, the difficulty to mount an attack can be reduced even further.

Key words: lattice attack, hidden number problem, closest vector problem, DSA, ECDSA

中图分类号:

TP309

余发江, 贾耀民. 对DSA和ECDSA的一种改进格攻击[J]. 信息网络安全, 2022, 22(2): 11-20.

YU Fajiang, JIA Yaomin. An Enhanced Lattice Attack to DSA and ECDSA Scheme[J]. Netinfo Security, 2022, 22(2): 11-20.

图/表 6

表1

图1

图2

图3

表2

表3

参考文献 28

[1]	FIPS PUB 186-4 Digital Signature Standard (DSS)[S]. USA: Department of Commerce/National Institute of Standards and Technology: Federal Information Processing Standards Publication, 2013.
[2]	ARANHA D F, NOVAES F R, TAKAHASHI A, et al. LadderLeak: Breaking ECDSA with Less than One Bit of Nonce Leakage[C]//ACM. 2020 ACM SIGSAC Conference on Computer and Communications Security (CCS’20), November 9-13, 2020, NY, USA. New York: ACM, 2020: 225-242.
[3]	MA Ziqiang, LI Bingyu, CAI Quanwei, et al. Applications and Developments of the Lattice Attack in Side Channel Attacks[C]//ACNS. ACNS 2020: Applied Cryptography and Network Security Workshops, February 5-9, 2020, New Orleans, USA. Heidelberg: Springer, 2020: 435-452.
[4]	BONEH D, VENKATESAN R. Hardness of Computing the Most Significant Bits of Secret Keys in Diffie-Hellman and Related Schemes[C]//Springer. CRYPTO’1996: Advances in Cryptology, August 18-22, 1996, California, USA. Heidelberg: Springer, 1996: 129-142.
[5]	MICCIANCIO D, GOLDWASSER S. Complexity of Lattice Problems[M]. Heidelberg: Springer, 2002.
[6]	LENSTRA A K, LENSTRA H W, LOVÁSZ L. Factoring Polynomials with Rational Coefficients[J]. Mathematische Annalen, 1982, 261(4):515-534. doi: 10.1007/BF01457454 URL
[7]	BABAI L. On Lovasz’ Lattice Reduction and the Nearest Lattice Point Problem[J]. Combinatorica, 1986, 6(1):1-13. doi: 10.1007/BF02579403 URL
[8]	HOWGRAVE-GRAHAM N A, SMART N P. Lattice Attacks on Digital Signature Schemes[J]. Designs, Codes and Cryptography, 2001, 23(3):283-290. doi: 10.1023/A:1011214926272 URL
[9]	NGUYEN P Q, SHPARLINSKI I E. The Insecurity of the Digital Signature Algorithm with Partially Known Nonces[J]. Journal of Cryptology, 2003, 15(3):151-176. doi: 10.1007/s00145-002-0021-3 URL
[10]	NGUYEN P Q, SHPARLINSKI I E. The Insecurity of the Elliptic Curve Digital Signature Algorithm with Partially Known Nonces[J]. Designs, Codes and Cryptography, 2001, 30(2):201-217. doi: 10.1023/A:1025436905711 URL
[11]	HLAVAC M, ROSA T. Extended Hidden Number Problem and Its Cryptanalytic Applications[C]//Springer. SAC 2006: Selected Areas in Cryptography, August 17-18, 2006, Montreal, Canada. Heidelberg: Springer, 2006: 114-133.
[12]	BENGER N, POL J V D, SMART N P, et al. Ooh Aah Just a Little Bit: A Small Amount of Side Channel Can Go a Long Way[C]//Springer. Cryptographic Hardware and Embedded Systems-CHES 2014, September 23-26, 2014, Busan, Republic of Korea. Heidelberg: Springer, 2014: 75-92.
[13]	POL J V D, SMART N P, YAROM Y. Just a Little Bit More[C]//Springer. Cryptographers’ Track at the RSA Conference (CT-RSA 2015), April 20-24, 2015, San Francisco, CA, USA. Heidelberg: Springer, 2015: 3-21.
[14]	FAN Shuqin, WANG Wenbo, CHENG Qingfeng. Attacking OpenSSL Implementation of ECDSA with a Few Signatures[C]//ACM. 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS’16), October 24-28, 2016, Vienna, Austria. New York: ACM, 2016: 1505-1515.
[15]	RYAN K. Return of the Hidden Number Problem: A Widespread and Novel Key Extraction Attack on ECDSA and DSA[EB/OL]. https://www.researchgate.net/publication/346703657_Return_of_the_Hidden_Number_Problem_A_Widespread_and_Novel_Key_Extraction_Attack_on_ECDSA_and_DSA, , 2018-11-20.
[16]	ARANHA D F, FOUQUE P A, GÉRARD B, et al. GLV/GLS Decomposition, Power Analysis, and Attacks on ECDSA Signatures with Single-bit Nonce Bias[C]//Springer. International Conference on the Theory and Application of Cryptology and Information Security 2014, December 7-11, 2014, Taibei, Taiwan, China. Heidelberg: Springer, 2014: 262-281.
[17]	GENKIN D, PACHMANOV L, PIPMAN I, et al. ECDSA Key Extraction from Mobile Devices via Nonintrusive Physical Side Channels[C]//ACM. 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS’16), October 24-28, 2016, Vienna, Austria. New York: ACM, 2016: 1626-1638.
[18]	BELGARRIC P, FOUQUE P A, MACARIO-RAT G, et al. Side-channel Analysis of Weierstrass and Koblitz Curve ECDSA on Android Smartphones[C]//Springer. Cryptographers’ Track at the RSA Conference 2016, February 29-March 4, 2016, San Francisco, CA, USA. Heidelberg: Springer, 2016: 232-256.
[19]	ZHANG Kaiyu, XU Sen, GU Dawu, et al. Practical Partial-nonce-exposure Attack on ECC Algorithm[C]//IEEE. 13th International Conference on Computational Intelligence and Security (CIS), December 15-18, 2017, Hong Kong, China. Piscataway: IEEE, 2017: 248-252.
[20]	CAO Weiqiong, FENG Jingyi, CHEN Hua, et al. Two Lattice-based Differential Fault Attacks Against ECDSA with wNAF Algorithm[C]//Springer. Information Security and Cryptology-ICISC 2015, November 25-27, 2015, Seoul, Republic of Korea. Heidelberg: Springer, 2015: 297-313.
[21]	NGUYEN P Q, TIBOUCHI M. Fault Analysis in Cryptography[M]. Heidelberg: Springer, 2012.
[22]	BRUMLEY B B, TUVERI N. Remote Timing Attacks Are Still Practical[C]//Springer. Computer Security-ESORICS 2011, September 12-14, 2011, Leuven, Belgium. Heidelberg: Springer, 2011: 355-371.
[23]	MOGHIMI D, SUNAR B, EISENBARTH T, et al. TPM-FAIL: TPM Meets Timing and Lattice Attacks[EB/OL]. https://arxiv.org/abs/1911.05673, 2019-11-13.
[24]	TIBOUCHI M. Attacks on (EC) DSA with Biased Nonces[EB/OL]. https://ecc2017.cs.ru.nl/slides/ecc2017-tibouchi.pdf, 2017-11-13.
[25]	POULAKIS D. New Lattice Attacks on DSA Schemes[J]. Journal of Mathematical Cryptology, 2016, 10(2):135-144.
[26]	ADAMOUDIS M, DRAZIOTIS K A, POULAKIS D. Enhancing an Attack to DSA Schemes[C]//Springer. International Conference on Algebraic Informatics (CAI 2019), June 30-July 4, 2019, Niš, Serbia. Heidelberg: Springer, 2019: 13-25.
[27]	ADAMOUDIS M, DRAZIOTIS K A, POULAKIS D. Attacking (EC) DSA with Partially Known Multiples of Nonces[J]. IACR Cryptol ePrint Archive, 2021, 35(10):347-356.
[28]	SUN Chao, ESPITAU T, TIBOUCHI M, et al. Guessing Bits: Improved Lattice Attacks on (EC)DSA[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 28(1):391-413.

已知比特数$l$	格的维度最小值$d$
1	5110
2	270
3	135

	仅前2 bit为0	仅前1 bit为0
DSA	76%	57%
ECDSA	89%	87%