基于一类受限存取结构上的量子秘密共享方案

doi:10.3969/j.issn.1671-1122.2023.08.003

信息网络安全 ›› 2023, Vol. 23 ›› Issue (8): 32-40.doi: 10.3969/j.issn.1671-1122.2023.08.003

基于一类受限存取结构上的量子秘密共享方案

李志慧(), 罗双双, 韦性佳

陕西师范大学数学与统计学院，西安 710119

收稿日期:2023-05-25 出版日期:2023-08-10 发布日期:2023-08-08
通讯作者: 李志慧 E-mail:lizhihui@snnu.edu.cn
作者简介:李志慧（1966—），女，陕西，教授，博士，主要研究方向为有限域和密码学|罗双双（1997—），女，黑龙江，硕士研究生，主要研究方向为密码学|韦性佳（1991—），男，甘肃，博士研究生，主要研究方向为密码学
基金资助:
国家自然科学基金(12071271)

Quantum Secret Sharing Schemes Based on a Class of Restricted Access Structures

LI Zhihui(), LUO Shuangshuang, WEI Xingjia

School of Mathematics and Statistics, Shaanxi Normal University, Xi'an 710119, China

Received:2023-05-25 Online:2023-08-10 Published:2023-08-08
Contact: LI Zhihui E-mail:lizhihui@snnu.edu.cn

摘要/Abstract

摘要：

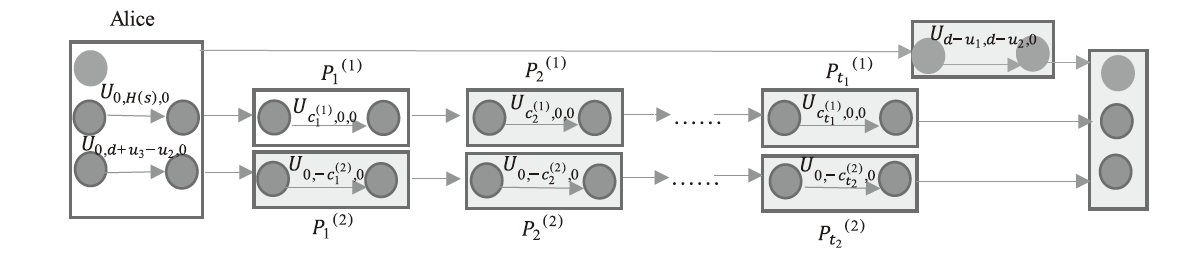
文章利用GHZ纠缠态的量子关联性设计了一个基于受限存取结构上的多方量子秘密共享方案。在方案中，首先，参与者被分成两个互不相交的子集，$d$维GHZ态的3个粒子作为信息载体，两个互不相交子集中的参与者分别持有GHZ态的第二和第三粒子，这些参与者将其秘密份额隐藏在经酉变换作用的量子态中；然后，子集中的参与者通过经典模型辅助可恢复秘密；最后，该方案与同类型方案相比，更节省量子资源，方案更简单，效率更高。

关键词: 存取结构, 单调张成方案, 量子秘密共享

Abstract:

In this paper, a multi-party quantum secret sharing based on a restricted access structure was designed using the quantum correlation of GHZ entangled state. In this paper, firstly, the participants were divided into two mutually disjoint subsets with three particles of the $d$-dimensional GHZ state as information carriers, and the participants in the two mutually disjoint subsets held the second and third particles of the GHZ state, respectively, and these participants hide their secret shares in quantum states which were acted the unitary transformations.Then, the participants in the subsets recovered the secret with the aid of the classical model. Finally, this scheme is more economical in terms of quantum resources compared to the same type of schemes, and the scheme is simpler and more efficient.

Key words: access structure, monotone span program, quantum secret sharing

中图分类号:

TP309

李志慧, 罗双双, 韦性佳. 基于一类受限存取结构上的量子秘密共享方案[J]. 信息网络安全, 2023, 23(8): 32-40.

LI Zhihui, LUO Shuangshuang, WEI Xingjia. Quantum Secret Sharing Schemes Based on a Class of Restricted Access Structures[J]. Netinfo Security, 2023, 23(8): 32-40.

图/表 2

参考文献 28

[1]	BENNETT C, BRASSARD G. WITHDRAWN: Quantum Cryptography:Public Key Distribution and Coin Tossing[C]//IEEE. Proceedings of IEEE International Conference on Computers,Systems, and Signal Processing. New York: IEEE, 1984, 175-179.
[2]	LO H K, CURTY M, QI M. Measurement-Device-Independent Quantum Key Distribution[EB/OL]. (2012-05-28)[2023-05-10]. https://doi.org/10.48550/arXiv.1109.1473.
[3]	TANG Yanlin, YIN Hualei, MA Xiongfeng, et al. Source Attack of Decoy-State Quantum Key Distribution Using Phase Information[EB/OL]. (2013-04-09)[2023-05-10]. https://doi.org/10.1103/PhysRevA.88.022308.
[4]	LO H K, MA Xiongfeng, CHEN Kai. Decoy State Quantum Key Distribution[EB/OL]. (2005-06-16)[2023-05-10]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.94.230504.
[5]	NAM S W, NORDHOLT J E, RICE P R, et al. Long Distance Decoy State Quantum Key Distribution in Optical Fiber[J]. Physical Review Letters, 2007, 98(1): 1-4.
[6]	WANG Xiangbin, YU Zongwen, HU Xiaolong. Twin-Field Quantum Key Distribution with Large Misalignment Error[EB/OL]. (2018-12-18)[2023-05-10]. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.98.062323.
[7]	MA Xiongfeng, ZENG Pei, ZHOU Hongyi. Phase-Matching Quantum Key Distribution[EB/OL]. (2018-05-15)[2023-05-10]. https://doi.org/10.1103/PhysRevX.8.031043.
[8]	PHOENIX S J, BARNEET S M, TOWNSEND P D, et al. Multi-User Quantum Cryptography on Optical Networks[J]. Journal of Modern Optics, 1995, 42(6), 1155-1163. doi: 10.1080/09500349514551001 URL
[9]	ALLATI A E, BAZ M E, HASSOUNI Y. Quantum Key Distribution via Tripartite Coherent States[J]. Quantum Information Processing, 2010, 10: 589-602. doi: 10.1007/s11128-010-0213-y URL
[10]	HWANG W Y, YUEN H P. Quantum Key Distribution with High Loss: Toward Global Secure Communication[EB/OL]. (2003-05-19)[2023-05-10]. https://doi.org/10.48550/arXiv.quant-ph/0211153.
[11]	HILLERY M, BUZEK V, BERTHIAUME A. Quantum Secret Sharing[EB/OL]. (1999-03-01)[2023-05-10]. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.59.1829.
[12]	PIVOLUSKA M, HUBER M, MALIK M. Layered Quantum Key Distribution[EB/OL]. (2017-11-23)[2023-05-10]. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.97.032312.
[13]	YAN Chenhong, LI Zhihui, LIU Lu, et al. Cheating Identifiable (k, n) Threshold Quantum Secret Sharing Scheme[J]. Quantum Information Processing, 2022, 21(8): 1-24. doi: 10.1007/s11128-021-03349-w
[14]	CABELLO A. Quantum Key Distribution in the Holevo Limit[EB/OL]. (2000-12-18)[2023-05-10]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.85.5635.
[15]	BENNETT C H. Quantum Cryptography Using Any Two Non-Orthogonal States[EB/OL]. (1992-05-25)[2023-05-10]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.68.3121.
[16]	GOLDENBERG L, VAIDMAN L. Quantum Cryptography Based on Orthogonal States[EB/OL]. (1995-02-25)[2023-05-10]. https://doi.org/10.48550/arXiv.quant-ph/9502021.
[17]	KOASHI M, IMOTO N. Quantum Cryptography Based on Split Transmission of One-Bit Information in Two Steps[EB/OL]. (1997-09-22)[2023-05-10]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.79.2383.
[18]	BAI Chenming, LI Zhihui, LI Yongming. Sequential Quantum Secret Sharing Using a Single Qubit[J]. Communications in Theoretical Physics, 2018, 69(5): 513-518. doi: 10.1088/0253-6102/69/5/513 URL
[19]	LI Lei, LI Zhi. A Verifiable Multiparty Quantum Key Agreement Based on Bivariate Polynomial[J]. Information Sciences, 2020, 521: 343-349. doi: 10.1016/j.ins.2020.02.057 URL
[20]	RAHAMAN R, PARKER M G. Quantum Scheme for Secret Sharing Based on Local Distinguishability[EB/OL]. (2015-02-20)[2023-05-10]. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.91.022330.
[21]	YANG Yinghui, GAO Fei, WU Xia, et al. Quantum Secret Sharing via Local Operations and Classical Communication[EB/OL]. (2015-11-20)[2023-05-10]. https://www.nature.com/articles/srep16967.
[22]	BAI Chenming, LI Zhihui, XU Tingting, et al. Quantum Secret Sharing Using the d-Dimensional GHZ State[J]. Quantum Information Processing, 2017, 16(3): 1-13. doi: 10.1007/s11128-016-1481-y URL
[23]	LU Changbin, MIAO Fuyou, HOU Junpeng, et al. A Verifiable Framework of Entanglement-Free Quantum Secret Sharing with Information-Theoretical Security[EB/OL]. (2019-12-03)[2023-05-10]. https://doi.org/10.1007/s11128-019-2509-x.
[24]	LI Fulin, HU Hang, ZHU Shixin, et al. A Verifiable (k, n)- Threshold Dynamic Quantum Secret Sharing Scheme[J]. Quantum Information Processing, 2022, 21(7), 259-268. doi: 10.1007/s11128-022-03617-3
[25]	KARTICK S, HARI O. Efficient Quantum Secret Sharing without a Trusted Player[J]. Quantum Information Processing, 2020, 19(2): 1-15. doi: 10.1007/s11128-019-2494-0
[26]	WEN Qiaoyan, GUO Fenzhuo, ZHU Fucheng. Design and Analysis of Quantum Confidential Communication Protocols[M]. Beijing: Science Press, 2009.
	温巧燕, 郭奋卓, 朱甫成. 量子保密通信方案的设计与分析[M]. 北京: 科学出版社, 2009.
[27]	LIU Chengji, LI Zhui, BAI Chenming, et al. Quantum Secret Sharing Scheme Based on Local Distinguishability of Orthogonal Seven-Qudit Entangled States[J]. International Journal of Theoretical Physics, 2018, 57(2): 428-442. doi: 10.1007/s10773-017-3574-5 URL
[28]	LI Zhihui, JIANG Xue, LIU Lu. Multi-Party Quantum Secret Sharing Based on GHZ State[EB/OL]. (2022-10-08)[2023-05-10]. https://doi.org/10.3390/e24101433.

	文献[20] 方案	文献[21] 方案	文献[27] 方案	文献[22] 方案	文献[28] 方案	本文方案
可实现门限	限制(2,$n$)	(2,$n$)	(6,7)	广义限制(2,$n$)	限制(2,$n$)	限制($t$,$n$)
所用信息量子态类型	$n$维 GHZ态	$n$维GHZ态	$7$维纠缠态	$n$维 GHZ态	$2$维GHZ态	$d$维 GHZ态
所用信息量子态个数	2	2	5	2	2	1
参与者分组	2组	—	—	2组	2组	2组
所用检测量子态类型	2维 GHZ态	$n$维GHZ态	单光子	单光子	单光子	单光子
所用检测量子态个数	$nL$	$nL$	$nu$	$nu$	$nL$	$\left( t+3 \right)u$
酉操作次数	0	0	0	0	0	$t+3$
测量次数	$n\left( v+L \right)$	$n\left( v+L \right)$	$n\left( v+u \right)$	$n\left( v+u \right)$	$n\left( v+L \right)$	1
信息效率	$\frac{v}{n\left( v+L \right)}$	$\frac{v}{n\left( v+L \right)}$	$\frac{v}{n\left( v+u \right)}$	$\frac{v}{n\left( v+u \right)}$	$\frac{v}{n\left( v+L \right)}$	$\frac{v}{\left( t+3 \right)\left( v+u \right)}$

基于一类受限存取结构上的量子秘密共享方案

Quantum Secret Sharing Schemes Based on a Class of Restricted Access Structures

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 2

参考文献 28

相关文章 7

编辑推荐

Metrics

本文评价

[1]	杨宇光, 卢嘉煜. 一种基于星型簇态的动态的分级的量子秘密共享协议[J]. 信息网络安全, 2023, 23(6): 34-42.
[2]	吕凯欣, 李志慧, 黑吉辽, 宋云. 一类图存取结构的最优信息率计算[J]. 信息网络安全, 2022, 22(4): 77-85.
[3]	刘璐, 李志慧, 芦殿军, 闫晨红. 基于线性码的量子秘密共享方案[J]. 信息网络安全, 2021, 21(8): 62-69.
[4]	刘晓芬, 陈晓峰, 连桂仁, 林崧. 基于d级单粒子的可认证多方量子秘密共享协议[J]. 信息网络安全, 2020, 20(3): 51-55.
[5]	刘成基, 李志慧, 司萌萌, 白晨明. 基于局域区分的六粒子正交纠缠态的量子秘密共享方案[J]. 信息网络安全, 2018, 18(4): 56-64.
[6]	李志慧, 徐廷廷, 张娜. 一类理想的存取结构的构造[J]. 信息网络安全, 2016, 16(5): 15-22.
[7]	程资, 靳俐荣, 石金晶. 基于RS码生成机制的(k,n)门限量子秘密共享方案[J]. 信息网络安全, 2016, 16(4): 44-49.