信息网络安全 ›› 2023, Vol. 23 ›› Issue (6): 34-42.doi: 10.3969/j.issn.1671-1122.2023.06.004
一种基于星型簇态的动态的分级的量子秘密共享协议
- 1.北京工业大学信息学部,北京 100124
2.北京市可信计算重点实验室,北京 100124
-
收稿日期:2023-03-31出版日期:2023-06-10发布日期:2023-06-20 -
通讯作者:杨宇光yangyang7357@bjut.edu.cn -
作者简介:杨宇光(1976—),女,河北,教授,博士,主要研究方向为信息安全|卢嘉煜(1998—),女,北京,硕士研究生,主要研究方向为抗量子计算密码 -
基金资助:国家自然科学基金(62071015)
A Dynamic and Hierarchical Quantum Secret Sharing Protocol Based on Starlike Cluster States
- 1. Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China
2. Beijing Key Laboratory of Trusted Computing, Beijing 100124, China
-
Received:2023-03-31Online:2023-06-10Published:2023-06-20
摘要:
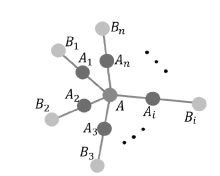
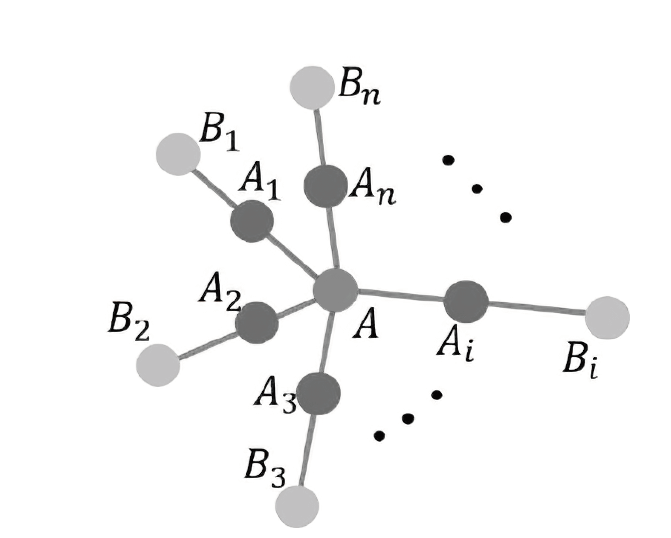
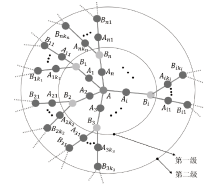
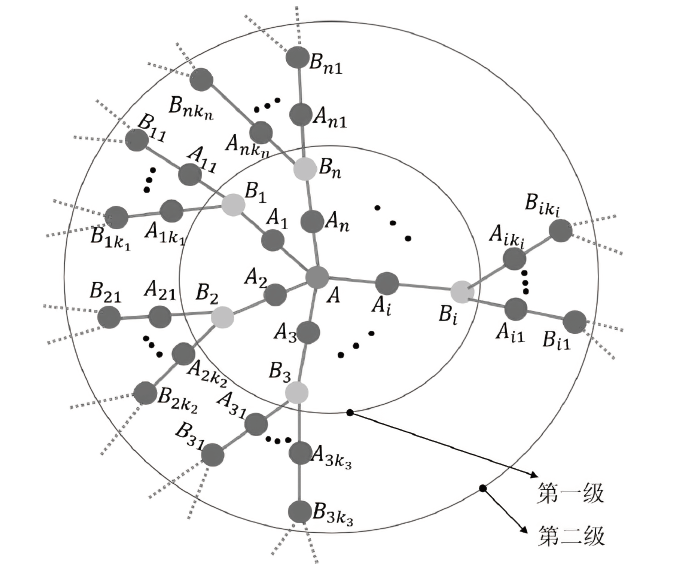
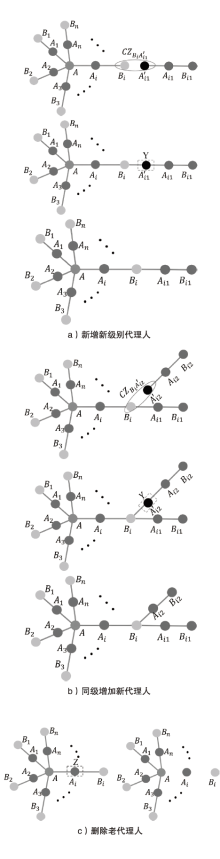
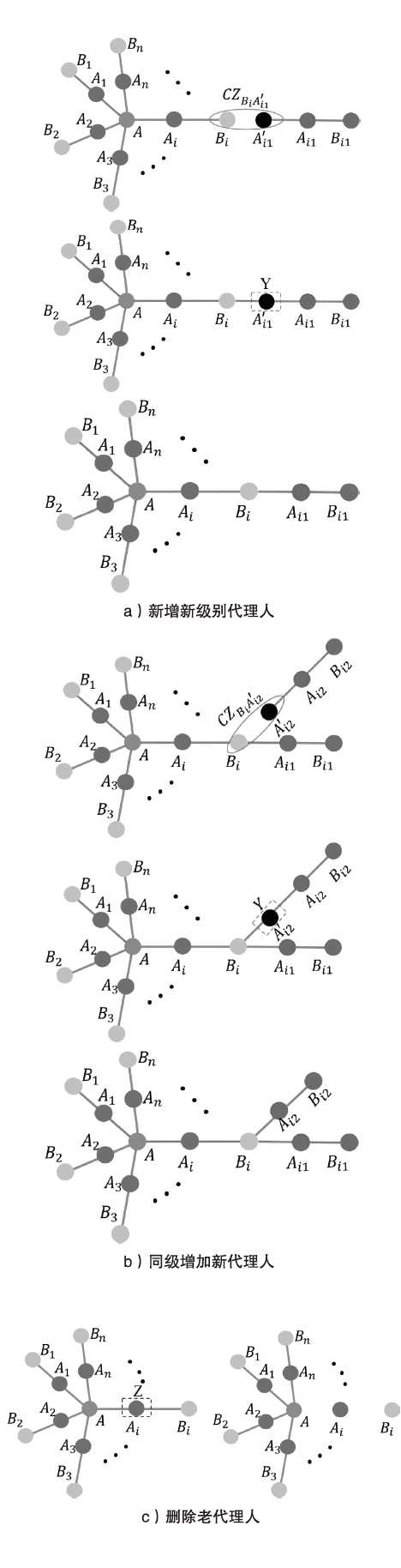
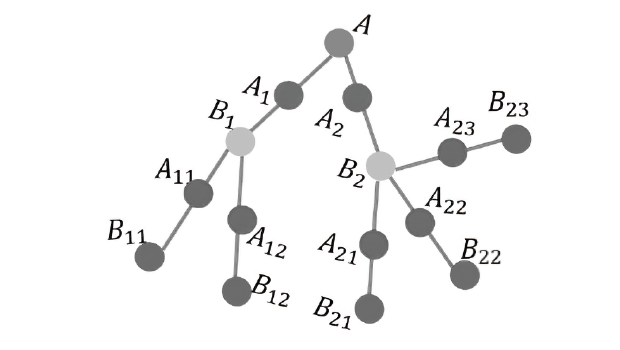
文章基于星型簇态构造了一种具有分级结构的簇态,利用所构造的簇态提出了一种动态、分级的量子秘密共享方案。秘密拥有者将具有分级结构的簇态粒子分别分发给每个代理人作为他的份额。被分配较高等级的粒子的代理人具有较高的权限而被分配较低等级的粒子的代理人具有较低的权限。每一等级的代理人都不能获得同等级、较高等级和较低等级的代理人的份额信息。由于簇态的可扩展性,所提出的分级的量子秘密共享方案是动态的,允许在同等级新增代理人、删除旧代理人以及不同等级之间代理人的升级和降级。最后,文章分析了所提出的协议的安全性。
中图分类号:
引用本文
杨宇光, 卢嘉煜. 一种基于星型簇态的动态的分级的量子秘密共享协议[J]. 信息网络安全, 2023, 23(6): 34-42.
YANG Yuguang, LU Jiayu. A Dynamic and Hierarchical Quantum Secret Sharing Protocol Based on Starlike Cluster States[J]. Netinfo Security, 2023, 23(6): 34-42.
表1
本文方案和其他方案的比较结果
| 协议 | 秘密 | 实现分级的方式 | 特征 |
|---|---|---|---|
| 文献[ | 经典 | 区块链 | 公平、分级 |
| 文献[ | 经典 | 线性齐次递归关系 | 分级 |
| 文献[ | 量子 | 指定参与者等级 | 分级 |
| 文献[ | 量子 | 指定参与者等级 | 分级 |
| 文献[ | 量子 | 指定参与者等级 | 分级 |
| 文献[ | 量子 | 特殊的高维纠缠态 | 分级 |
| 文献[ | 量子 | 线性代数技术 | 分级 |
| 文献[ | 量子 | 指定参与者等级 | 分级 |
| 文献[ | 量子 | 树形 | 动态、分级、可扩展、可控 |
| 文献[ | 量子 | 多尺度纠缠重整化ansatz | 动态、分级、可扩展、可控 |
| 本文协议 | 量子 | 星型簇态 | 动态、分级、可扩展、可控 |
表1
| [1] |
SHAMIR A. How to Share a Secret[J]. Commun ACM, 1979, 22(11): 612-613.
doi: 10.1145/359168.359176 URL |
| [2] | BLAKLEY G R. Safeguarding Cryptographic Keys[C]// IEEE. American Federation of Information Processing Societies-Conference Proceedings. New York: IEEE, 1979: 313-317. |
| [3] | KOTHARI S C. Generalized Linear Threshold Scheme[C]// Springer. Advances in Cryptology. Berlin:Springer, 1984: 231-241. |
| [4] |
TASSA T. Hierarchical Threshold Secret Sharing[J]. Cryptol, 2007, 20: 1-27.
doi: 10.1080/0161-119691884735 URL |
| [5] |
FARRAS O, PADRO C. Ideal Hierarchical Secret Sharing Schemes[J]. IEEE Transactions on Information Theory, 2012, 58(5): 3273-3286.
doi: 10.1109/TIT.2011.2182034 URL |
| [6] | TRAVERSO G, DEMIREL D, BUCHMANN J. Dynamic and Verifiable Hierarchical Secret Sharing[C]// Springer. International Conference on Information Theoretic Security. Berlin:Springer, 2016: 299-319. |
| [7] |
CHEN Qi, TANG Chunming, LIN Zhiqiang. Efficient Explicit Constructions of Multipartite Secret Sharing Schemes[J]. IEEE Transactions on Information Theory, 2021, 68: 601-636.
doi: 10.1109/TIT.2021.3123102 URL |
| [8] |
ZHANG En, LI Ming, YIU S, et al. Fair Hierarchical Secret Sharing Scheme Based on Smart Contract[J]. Information Sciences, 2021, 546: 166-179.
doi: 10.1016/j.ins.2020.07.032 URL |
| [9] |
YUAN Jiangtao, YANG Jing, WANG Chenyu, et al. A New Efficient Hierarchical Multi-Secret Sharing Scheme Based on Linear Homogeneous Recurrence Relations[J]. Information Sciences, 2022, 592: 36-49.
doi: 10.1016/j.ins.2022.01.053 URL |
| [10] |
WANG Xinwen, XIA Lixin, WANG Zhiyong, et al. Hierarchical Quantum-Information Splitting[J]. Optics Communications, 2010, 283(6): 1196-1199.
doi: 10.1016/j.optcom.2009.11.015 URL |
| [11] |
WANG Xinwen, ZHANG Dengyu, TANG Shiqing, et al. Hierarchical Quantum Information Splitting with Six-Photon Cluster States[J]. International Journal of Theoretical Physics, 2010, 49: 2691-2697.
doi: 10.1007/s10773-010-0461-8 URL |
| [12] |
WANG Xinwen, ZHANG Dengyu, TANG Shiqing, et al. Multiparty Hierarchical Quantum-Information Splitting[EB/OL]. (2011-09-19)[2023-03-20]. https://doi.org/10.48550/arXiv.1101.3700.
doi: https://doi.org/10.48550/arXiv.1101.3700 |
| [13] |
BAI Mingqiang, MO Zhiwen. Hierarchical Quantum Information Splitting with Eight-Qubit Cluster States[J]. Quantum Information Processing, 2013, 12: 1053-1064.
doi: 10.1007/s11128-012-0440-5 URL |
| [14] | PENG Jiayin, MO Zhiwen. Hierarchical and Probabilistic Quantum State Sharing with a Nonmaximally Four-Qubit Cluster State[J]. International Journal of Quantum Information, 2013, 11(1): 135-145. |
| [15] |
XU Gang, WANG Cong, YANG Yixian. Hierarchical Quantum Information Splitting of an Arbitrary Two-Qubit State via the Cluster State[J]. Quantum Information Processing, 2014, 13: 43-57.
doi: 10.1007/s11128-013-0670-1 URL |
| [16] |
ZHA Xinwei, MIAO Ning, WANG Huifang. Hierarchical Quantum Information Splitting of an Arbitrary Two-Qubit Using a Single Quantum Resource[J]. International Journal Theoretical Physics, 2019, 58: 2428-2434.
doi: 10.1007/s10773-019-04134-3 |
| [17] | PENG Jiayin, BAI Mingqiang, MO Zhiwen. Hierarchical and Probabilistic Quantum State Sharing via a Non-Maximally Entangled $|\chi $ State[EB/OL]. (2014-12-03)[2023-03-20]. http://www.cnki.com.cn/Article/CJFDTotal-ZGWL201401011.htm. |
| [18] | QIN Huawang, TANG W K S, TSO R. Hierarchical Quantum Secret Sharing Based on Special High-Dimensional Entangled State[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2020, 26(3): 53-68. |
| [19] |
MISHRA S, SHUKLA C, PATHAK A, et al. An Integrated Hierarchical Dynamic Quantum Secret Sharing Protocol[J]. International Journal of Theoretical Physics, 2015, 54(9): 3143-3154.
doi: 10.1007/s10773-015-2552-z URL |
| [20] |
LAI Hong, PIEPRZYK J, PAN Lei. Dynamic Hierarchical Quantum Secret Sharing Based on the Multiscale Entanglement Renormalization Ansatz[EB/OL]. (2022-10-18)[2023-03-20]. https://doi.org/10.1103/PhysRevA.106.052403.
doi: https://doi.org/10.1103/PhysRevA.106.052403 |
| [21] | CHEN Qing, CHENG Jianhua, WANG Kelin, et al. Efficient Construction of Two-Dimensional Cluster States with Probabilistic Quantum Gates[J]. Physical Review A, 2006, 73(1): 23-28. |
| [22] | FUJII K, TOKUNAGA Y. Fault-Tolerant Topological One-Way Quantum Computation with Probabilistic Two-Qubit Gates[J]. Physical Review Letters, 2010, 105(25): 1-5. |
| [23] | FUJII K, YAMAMOTO K. Topological One-Way Quantum Computation on Verified Logical Cluster States[J]. Physical Review A, 2010, 82(6): 1-4. |
| [24] |
JIA Hengyue, WEN Qiaoyan, GAO Fei, et al. Dynamic Quantum Secret Sharing[J]. Physics Letters A, 2012, 376(10), 1035-1041.
doi: 10.1016/j.physleta.2012.02.004 URL |
| [25] |
YANG Yuguang, LIU Zhichao, LI Jian, et al. Theoretically Extensible Quantum Digital Signature with Starlike Cluster States[J]. Quantum Information Processing, 2017, 16(1): 1-15.
doi: 10.1007/s11128-016-1481-y URL |
| [26] | HEIN M, EISERT J, and Briegel H J. Multi-Party Entanglement in Graph States[EB/OL]. (2005-08-09)[2023-03-20]. https://arxiv.org/pdf/quant-ph/0307130. pdf. |
| [27] |
JENNEWEIN T, SIMON C, WWIHS G, et al. Quantum Cryptography with Entangled Photons. Physical Review Letters, 2000, 84(20): 4729-4732.
pmid: 10990782 |
| [28] |
GOBBY C, YUAN Zhiliang, SHIELDS A J. Quantum Key Distribution over 122km Standard Telecom Fiber[J]. Applied Physics Letters, 2004, 84: 3762-3764.
doi: 10.1063/1.1738173 URL |
| [29] | JIA Hengyue, LIU Kangting, WU Xia, et al. Quantum Cheque Protocol Based on Bell States[J]. Netinfo Security, 2022, 22(6): 38-43. |
| 贾恒越, 刘康婷, 武霞, 等. 基于Bell态的量子支票协议[J]. 信息网络安全, 2022, 22(6): 38-43. | |
| [30] | LIU Lu, LI Zhihui, LU Dianjun, et al. Quantum Secret Sharing Scheme Based on Linear Codes[J]. Netinfo Security, 2021, 21(8): 62-69. |
| 刘璐, 李志慧, 芦殿军, 等. 基于线性码的量子秘密共享方案[J]. 信息网络安全, 2021, 21(8): 62-69. | |
| [31] | XIE Sijiang, GAO Qiong, FENG Yan. A Multiple Paths Routing Scheme with Least Number of Public Nodes Based on Trust Relaying Quantum Key Distribution Network[J]. Netinfo Security, 2021, 21(7): 35-42. |
| 谢四江, 高琼, 冯雁. 基于可信中继量子密钥分发网络的最少公共节点多路径路由方案[J]. 信息网络安全, 2021, 21(7): 35-42. |
| [1] | 郭宝霞, 王佳慧, 马利民, 张伟. 基于零信任的敏感数据动态访问控制模型研究[J]. 信息网络安全, 2022, 22(6): 86-93. |
| [2] | 张伟, 徐智刚, 陈云芳, 黄海平. 一种基于动态Docker的SDN蜜网设计与实现[J]. 信息网络安全, 2022, 22(4): 40-48. |
| [3] | 易铮阁, 袁文勇, 李瑞峰, 杨晓元. 一种支持动态操作的身份基云存储方案[J]. 信息网络安全, 2022, 22(2): 86-95. |
| [4] | 刘璐, 李志慧, 芦殿军, 闫晨红. 基于线性码的量子秘密共享方案[J]. 信息网络安全, 2021, 21(8): 62-69. |
| [5] | 王刚, 王志屹, 张恩宁, 马润年. 多阶段平台动态防御的信号博弈模型及迁移策略[J]. 信息网络安全, 2021, 21(5): 48-57. |
| [6] | 黄长慧, 胡光俊, 李海威. 基于URL智能白名单的Web应用未知威胁阻断技术研究[J]. 信息网络安全, 2021, 21(3): 1-6. |
| [7] | 丁建立, 陈盼, 马勇. 基于泛化FPE加密的民航旅客信息动态脱敏方法研究[J]. 信息网络安全, 2021, 21(2): 45-52. |
| [8] | 魏占祯, 彭星源, 赵洪. SDN中基于用户信任度的资源访问控制方案[J]. 信息网络安全, 2021, 21(10): 33-40. |
| [9] | 刘红, 张越今, 赵文霞, 杨牧. 多维度数据分级分类安全管理框架[J]. 信息网络安全, 2021, 21(10): 48-53. |
| [10] | 王鹃, 杨泓远, 樊成阳. 一种基于多阶段攻击响应的SDN动态蜜罐[J]. 信息网络安全, 2021, 21(1): 27-40. |
| [11] | 陈福才, 周梦丽, 刘文彦, 梁浩. 云环境下面向拟态防御的反馈控制方法[J]. 信息网络安全, 2021, 21(1): 49-56. |
| [12] | 周枝凝, 王斌君, 翟一鸣, 仝鑫. 基于ALBERT动态词向量的垃圾邮件过滤模型[J]. 信息网络安全, 2020, 20(9): 107-111. |
| [13] | 夏天雨, 顾益军. 一种基于改进DynamicTriad模型的动态链路预测方法[J]. 信息网络安全, 2020, 20(9): 97-101. |
| [14] | 郎为民, 马卫国, 张寅, 姚晋芳. 一种支持数据所有权动态管理的数据去重方案[J]. 信息网络安全, 2020, 20(6): 1-9. |
| [15] | 金辉, 张红旗, 张传富, 胡浩. 复杂网络中基于QRD的主动防御决策方法研究[J]. 信息网络安全, 2020, 20(5): 72-82. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||