信息网络安全 ›› 2025, Vol. 25 ›› Issue (3): 467-477.doi: 10.3969/j.issn.1671-1122.2025.03.009
基于量子卷积神经网络的ARX分组密码区分器
- 湖北大学网络空间安全学院,武汉 430062
-
收稿日期:2024-12-19出版日期:2025-03-10发布日期:2025-03-26 -
通讯作者:李丽莎 E-mail:Li_sha_Li@163.com -
作者简介:秦广雪(2001—),男,河南,硕士研究生,主要研究方向为对称密码算法安全性分析|李丽莎(1992—),女,湖北,副教授,博士,主要研究方向为密码学 -
基金资助:国家自然科学基金(12101207);湖北省重点研发计划(2023BAB171)
ARX Block Cipher Distinguisher Based on Quantum Convolutional Neural Network
- School of Cyber Science and Technology, Hubei University, Wuhan 430062, China
-
Received:2024-12-19Online:2025-03-10Published:2025-03-26 -
Contact:LI Lisha E-mail:Li_sha_Li@163.com
摘要:
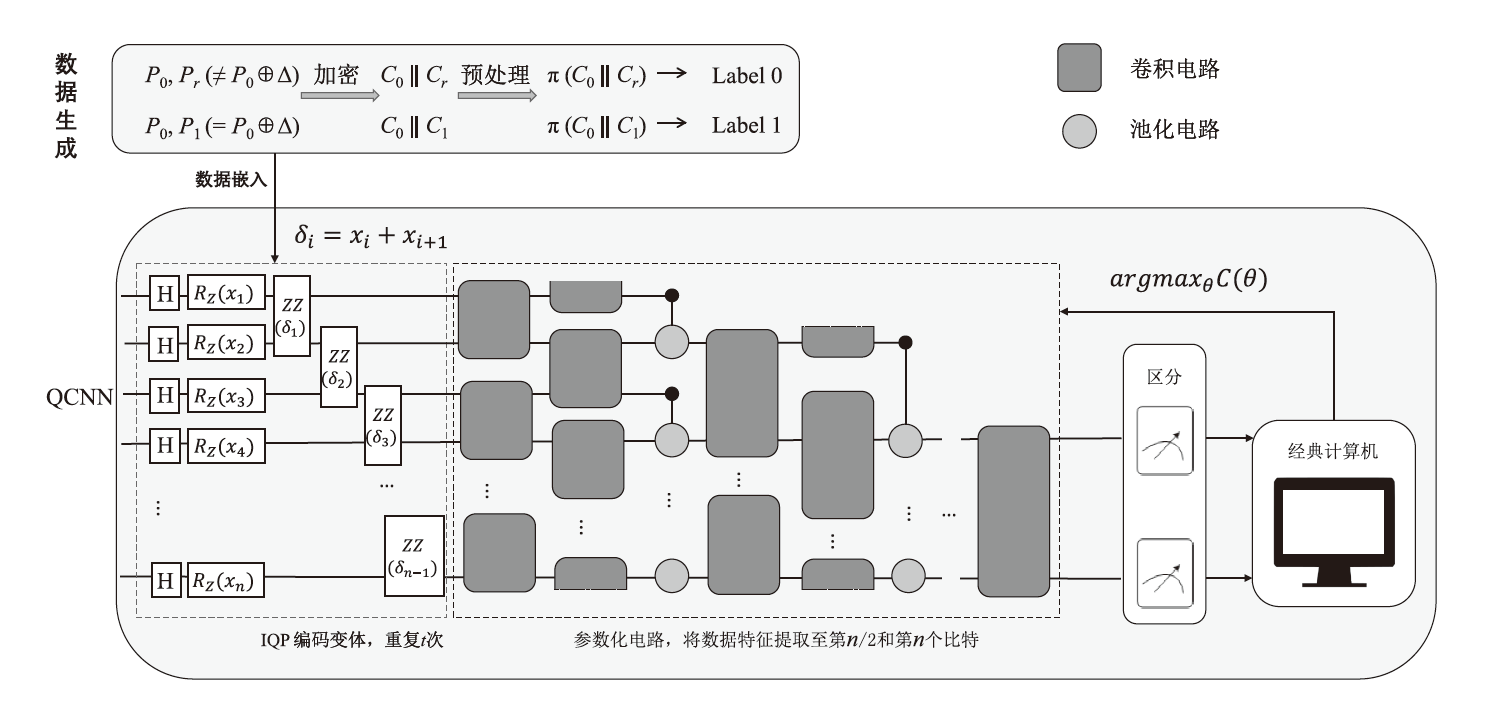
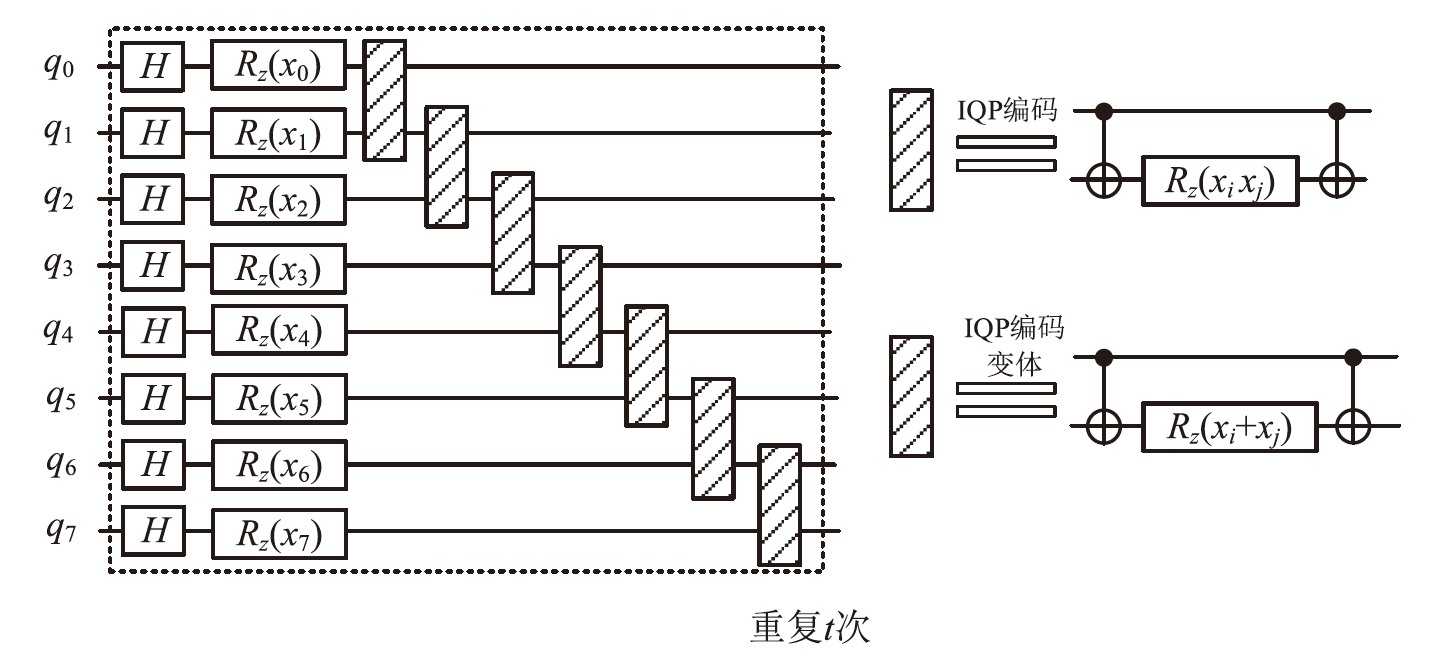
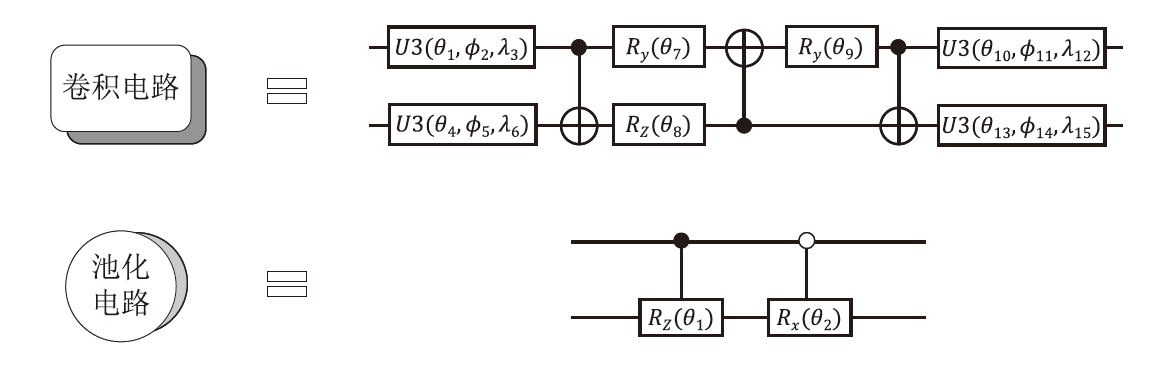
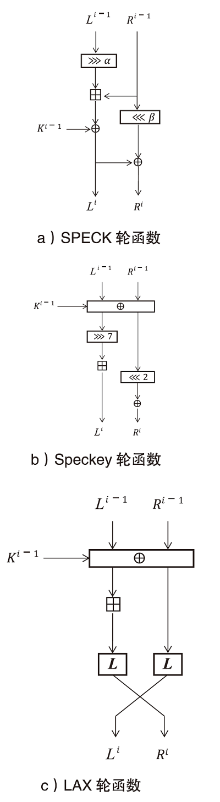
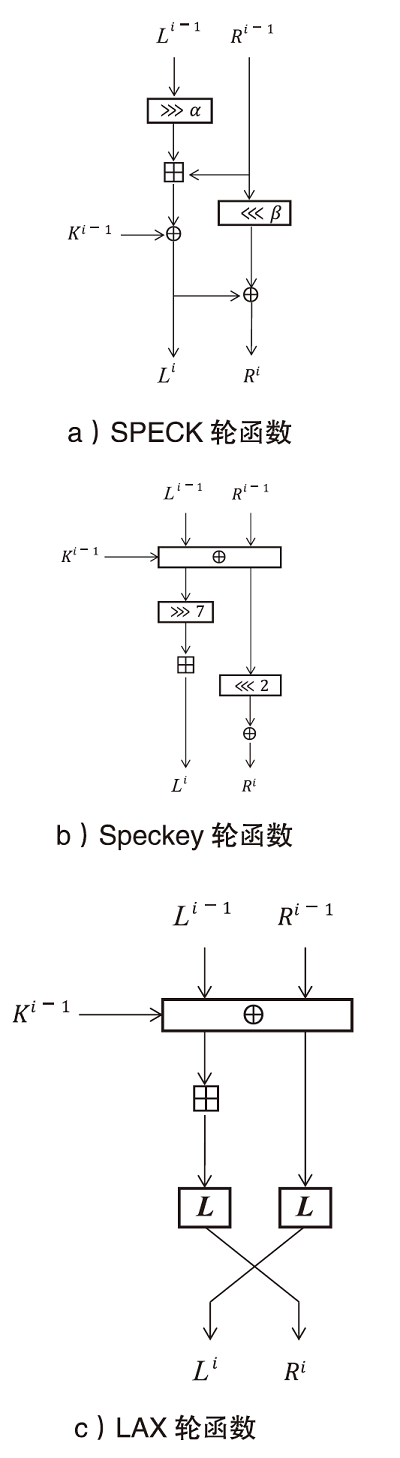
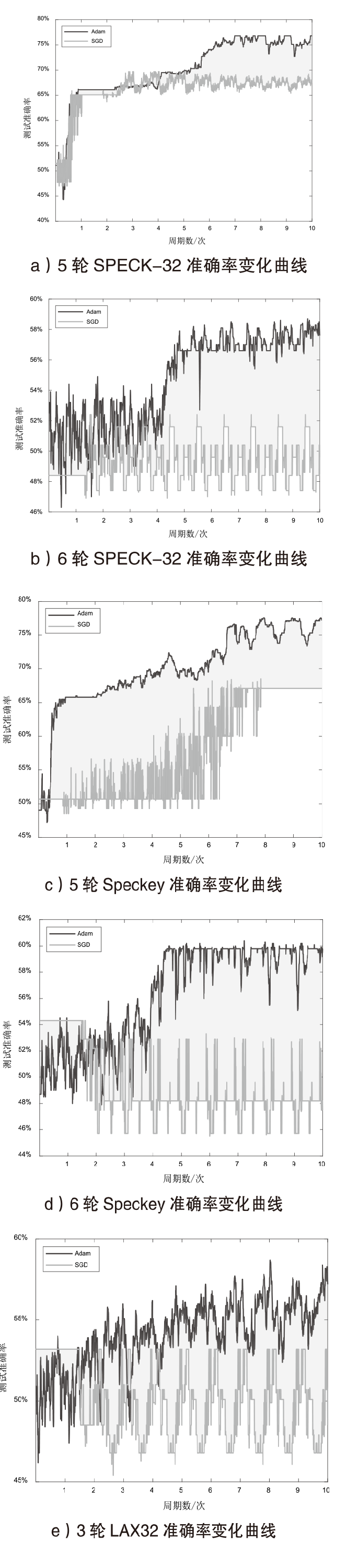
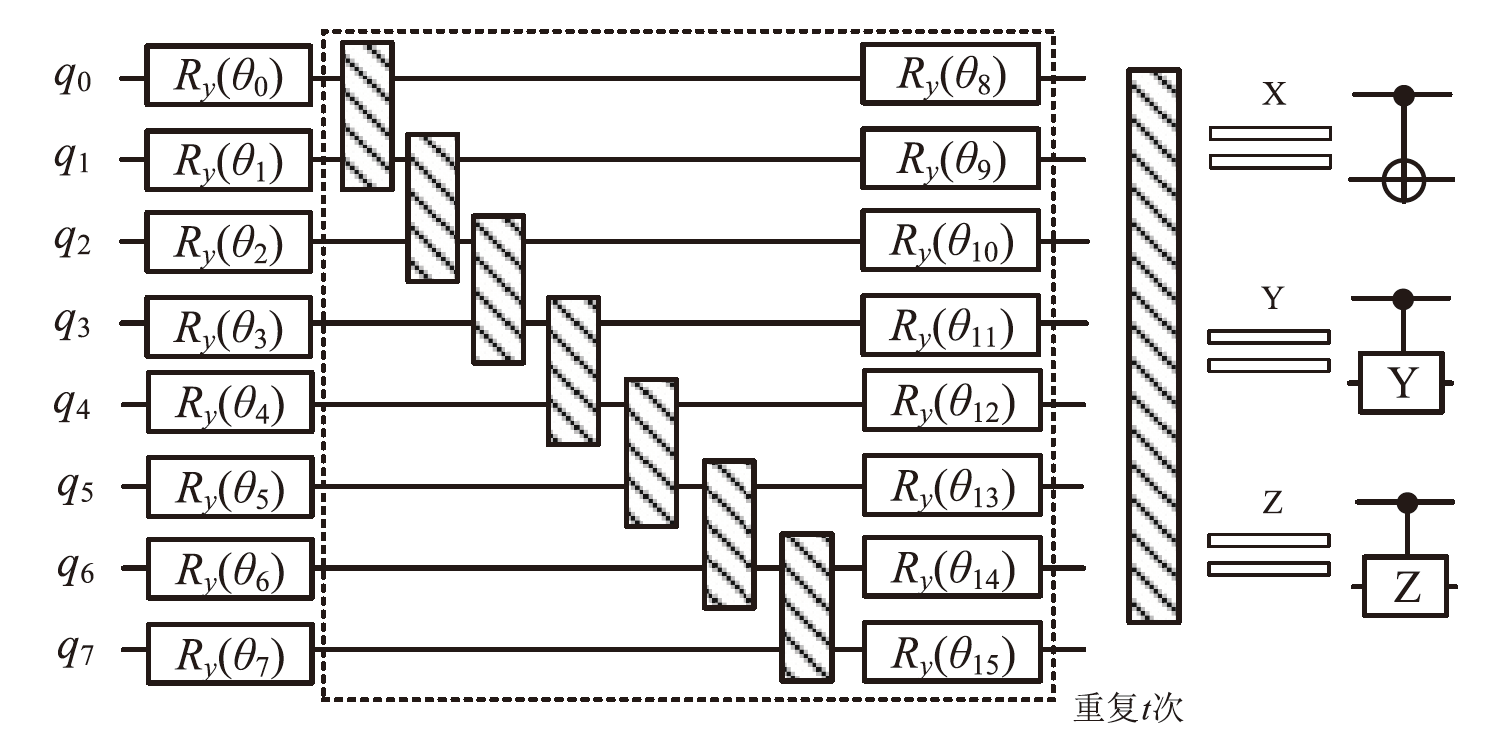
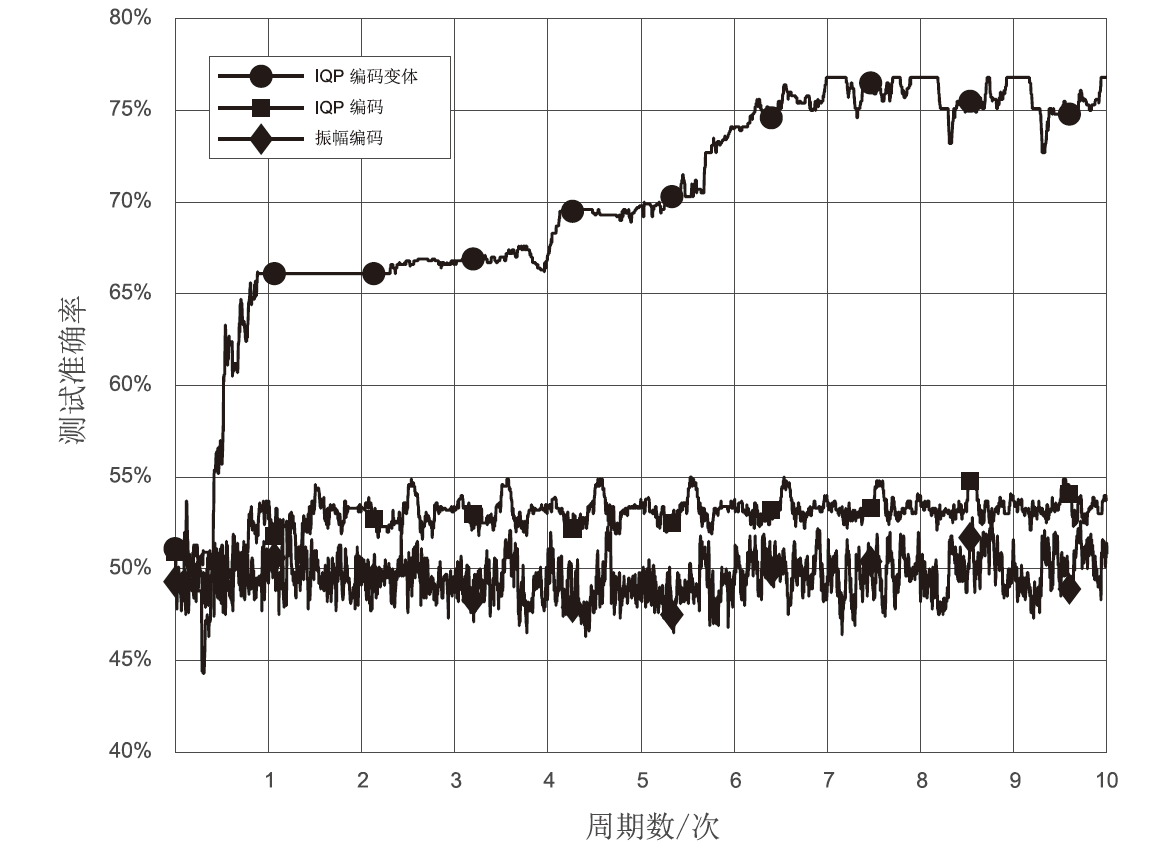
随着量子计算机的发展,量子神经网络技术不断取得新突破。尽管当前量子计算环境受限,但探索量子神经网络的潜在应用对未来科学技术发展具有重要意义。量子卷积神经网络结合量子计算的优势和神经网络强大的特征提取能力,在二分类任务上表现优异。文章提出一种量子卷积神经区分器,数据特征之间不分块而是作为一个整体编码到量子电路,然后训练参数化量子卷积电路。以SPECK-32为例,使用8个量子比特运行5轮的准确率为76.8%,超越了同等资源条件下的经典区分器,并成功运行到第6轮。文章对比了卷积电路和硬件高效Ansatz作为训练电路的量子神经区分器,结果表明前者具有更高的效率。此外,文章所提区分器成功运行了减轮的Speckey、LAX32、SIMON-32和SIMECK-32算法。最后,分析了影响量子卷积神经区分器性能的因素。
中图分类号:
引用本文
秦广雪, 李丽莎. 基于量子卷积神经网络的ARX分组密码区分器[J]. 信息网络安全, 2025, 25(3): 467-477.
QIN Guangxue, LI Lisha. ARX Block Cipher Distinguisher Based on Quantum Convolutional Neural Network[J]. Netinfo Security, 2025, 25(3): 467-477.
使用本文
表1
5轮SPECK-32的两种区分器性能对比结果
| 方法 | 量子比特数 /个 | 编码方法 | 参数 数量 /个 | 数据大小/个 (训练,测试) | 周期数 /次 | 批大小 /个 | 训练 准确率 | 测试 准确率 |
|---|---|---|---|---|---|---|---|---|
| 文献[ | 16 | 基态编码 | 385 | 213.8727, 29.9660 | 10 | 32 | 52% | 53% |
| 本文 | 8 | IQP编码变体 | 213 | 213.8727, 29.9660 | 10 | 32 | 75.9% | 76.8% |
| Constrained C | — | — | 4353 | 同本文 | 同本文 | 同本文 | 79% | 76% |
| 文献[ (C1) | — | — | 100897 | 223.2534, 219.9316 | 200 | 5000 | 93% | 93% |
| 文献[ (C2) | — | — | 自适应调整 | 223.2534, 219.9316 | 10 | 500 | 99% (最大) | 99% (最大) |
表2
各算法的量子和经典神经区分器对比
| 算法 | 轮数 /轮 | 模式 | 学习率 | 训练数据量/个 | 周期数/次 | 批大小/个 | 测试准确率 |
|---|---|---|---|---|---|---|---|
| SPECK-32 | 5 | Q | 0.1% | 213.8727 | 10 | 32 | 76.8% |
| 5 | C | — | 223.2534 | 10 | 500 | 99%(最大)[ | |
| SPECK-32 | 6 | Q | 1% | 213.8727 | 10 | 64 | 58.5% |
| 6 | C | — | 223.2534 | 10 | 500 | 98%(最大)[ | |
| Speckey | 5 | Q | 0.1% | 213.8727 | 10 | 32 | 77.2% |
| 5 | C | — | 223.2534 | 100 | 5000 | 97.4%(最佳)[ | |
| Speckey | 6 | Q | 1% | 213.8727 | 10 | 64 | 59.8% |
| 6 | C | — | 223.2534 | 100 | 5000 | 87.8%(最佳)[ | |
| LAX32 | 3 | Q | 1% | 213.8727 | 10 | 64 | 58.3% |
| 3 | C | — | 223.2534 | 100 | 5000 | 90.2%(最佳)[ |
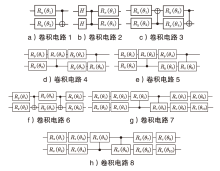
表5
不同卷积电路的5轮SPECK-32区分器对比
| 电路 | 参数电路量子门数/个 | 参数数量/个 | 训练准确率 | 测试准确率 |
|---|---|---|---|---|
| 卷积电路1 | 63 | 38 | 50.10% | 46.50% |
| 卷积电路2 | 89 | 51 | 65.00% | 61.90% |
| 卷积电路3 | 102 | 64 | 58.10% | 60.60% |
| 卷积电路4 | 102 | 90 | 65.20% | 64.70% |
| 卷积电路5 | 102 | 90 | 65.10% | 66.50% |
| 卷积电路6 | 128 | 90 | 65.40% | 64.90% |
| 卷积电路7 | 154 | 142 | 64.80% | 66.80% |
| 卷积电路8 | 154 | 142 | 64.60% | 67.50% |
| 156 | 213 | 75.90% | 76.80% |
| [1] | BIAMONTE J, WITTEK P, PANCOTTI N, et al. Quantum Machine Learning[J]. Nature, 2017, 549(7671): 195-202. |
| [2] | RUAN Yue, CHEN Hanwu, LIU Zhihao, et al. Quantum Principal Component Analysis Algorithm[J]. Chinese Journal of Computers, 2014, 37(3): 666-676. |
| [3] | LI Zhaokai, LIU Xiaomei, XU Nanyang, et al. Experimental Realization of a Quantum Support Vector Machine[EB/OL]. (2015-04-08)[2024-11-19]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.114.140504. |
| [4] | DANG Yijie, JIANG Nan, HU Hao, et al. Image Classification Based on Quantum K-Nearest-Neighbor Algorithm[J]. Quantum Information Processing, 2018, 17: 1-18. |
| [5] | DWIVEDI K, NIGAM A. Quantum Deep Learning for Phoniatrics Biomarker Based Disease Detection Deep Learning Model for Disease Detection by Phoniatrics Biomarkers Using Quantum Computation[C]// IEEE. 2nd International Conference on Data, Engineering and Applications (IDEA). New York: IEEE, 2020: 1-8. |
| [6] | DONG Yumin, FU Yanying, LIU Hengrui, et al. An Improved Hybrid Quantum-Classical Convolutional Neural Network for Multi-Class Brain Tumor MRI Classification[EB/OL]. (2023-02-14)[2024-11-19]. https://pubs.aip.org/aip/jap/article-abstract/133/6/064401/2872018. |
| [7] | ZOUFAL C, LUCCHI A, WOERNER S. Variational Quantum Boltzmann Machines[J]. Quantum Machine Intelligence, 2021, 3: 1-15. |
| [8] | STAMATOPOULOS N, EGGER D J, SUN Yue, et al. Option Pricing Using Quantum Computers[EB/OL]. (2020-07-02)[2024-11-19]. https://arxiv.org/abs/1905.02666v5. |
| [9] | WANG Jian, ZHANG Rui, JIANG Nan. Survey on Quantum Machine Learning[J]. Journal of Software, 2024, 35(8): 3843-3877. |
| 王健, 张蕊, 姜楠. 量子机器学习综述[J]. 软件学报, 2024, 35(8): 3843-3877. | |
| [10] | WIEBE N, KAPOOR A, SVORE K M. Quantum Deep Learning[EB/OL]. (2014-12-10)[2024-11-19]. https://arxiv.org/abs/1412.3489. |
| [11] | LLOYD S, WEEDBROOK C. Quantum Generative Adversarial Learning[EB/OL]. (2018-07-26)[2024-11-19]. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.040502. |
| [12] | CHEN S Y C, YANG C H H, QI Jun, et al. Variational Quantum Circuits for Deep Reinforcement Learning[J]. IEEE Access, 2020, 8: 141007-141024. |
| [13] |
CONG I, CHOI S, LUKIN M D. Quantum Convolutional Neural Networks[J]. Nature Physics, 2019, 15(12): 1273-1278.
doi: 10.1038/s41567-019-0648-8 |
| [14] | KAK S C. Quantum Neural Computing[J]. Advances in Imaging and Electron Physics. 1995, 94: 259-313. |
| [15] |
ABBAS A, SUTTER D, ZOUFAL C, et al. The Power of Quantum Neural Networks[J]. Nature Computational Science, 2021, 1(6): 403-409.
doi: 10.1038/s43588-021-00084-1 pmid: 38217237 |
| [16] | KIM H, JANG K, LIM S, et al. Quantum Neural Network Based Distinguisher on SPECK-32/64[EB/OL]. (2023-06-18)[2024-11-19]. https://www.mdpi.com/1424-8220/23/12/5683. |
| [17] | HUR T, KIM L, PARK D K. Quantum Convolutional Neural Network for Classical Data Classification[EB/OL]. (2022-02-11)[2024-11-19]. https://arxiv.org/abs/2108.00661. |
| [18] | GOHR A. Improving Attacks on Round-Reduced SPECK32/64 Using Deep Learning[EB/OL]. (2019-08-15)[2024-11-19]. https://ia.cr/2019/037. |
| [19] | CHEN Yi, YU Hongbo. A New Neural Distinguisher Model Considering Derived Features from Multiple Ciphertext Pairs[EB/OL]. (2021-03-09)[2024-11-19]. https://ia.cr/2021/310. |
| [20] | BENAMIRA A, GERAULT D, PEYRIN T, et al. A Deeper Look at Machine Learning-Based Cryptanalysis[EB/OL]. (2021-03-22)[2024-12-19]. https://ia.cr/2021/287. |
| [21] | BAKSI A, BREIER J, CHEN Yi, et al. Machine Learning Assisted Differential Distinguishers for Lightweight Ciphers (Extended Version)[EB/OL]. (2020-12-02)[2024-11-19]. https://ia.cr/2020/571. |
| [22] | HOU Zezhou, REN Jiongjiong, CHEN Shaozhen. Cryptanalysis of Round-Reduced SIMON32 Based on Deep Learning[EB/OL]. (2021-03-18)[2024-11-19]. https://ia.cr/2021/362. |
| [23] | YADAV T, KUMAR M. Differential-ML Distinguisher: Machine Learning Based Generic Extension for Differential Cryptanalysis[EB/OL]. (2020-10-29)[2024-11-19]. https://ia.cr/2020/913. |
| [24] | LU Jinyu, LIU Guoqiang, SUN Bing, et al. Improved (Related-Key) Differential-Based Neural Distinguishers for SIMON and Simeck Block Ciphers[J]. The Computer Journal, 2024, 67(2): 537-547. |
| [25] | RAJAN R, ROY R K, SEN D, et al. Deep Learning-Based Differential Distinguisher for Lightweight Cipher GIFT-COFB[C]// IPSCTM. Proceedings of MISS 2021. Heidelberg: Springer, 2022: 397-406. |
| [26] | YANG Xiaoxue, CHEN Jie, HAN Lidong. Application of Deep Learning in Differential Cryptanalysis of ARX Block Ciphers[J]. Journal of Cryptologic Research, 2022, 9(5): 923-935. |
| 杨小雪, 陈杰, 韩立东. 深度学习在 ARX 分组密码差分分析的应用[J]. 密码学报, 2022, 9(5): 923-935. | |
| [27] | HAVLÍČEK V, CÓRCOLES A D, TEMME K, et al. Supervised Learning with Quantum-Enhanced Feature Spaces[J]. Nature, 2019, 567(7747): 209-212. |
| [28] | BIRYUKOV A, VELICHKOV V, LE C Y. Automatic Search for the Best Trails in ARX: Application to Block Cipher Speck[EB/OL]. (2016-04-25)[2024-11-19]. https://ia.cr/2016/409. |
| [29] | DINU D, PERRIN L, UDOVENKO A, et al. Design Strategies for ARX with Provable Bounds: Sparx and LAX (Full Version)[EB/OL]. (2021-05-31)[2024-11-19]. https://ia.cr/2016/984. |
| [30] | BEAULIEU R, SHORS D, SMITH J, et al. The SIMON and SPECK Lightweight Block Ciphers[C]// IEEE. 52nd ACM/EDAC/IEEE Design Automation Conference (DAC). New York: IEEE, 2015: 1-6. |
| [31] | YANG Gangqiang, ZHU Bo, SUDER V, et al. The Simeck Family of Lightweight Block Ciphers[EB/OL]. (2015-06-30)[2024-11-19]. https://ia.cr/2015/612. |
| [1] | 张兴兰, 李登祥. 基于Grover量子搜索算法的MD5碰撞攻击模型[J]. 信息网络安全, 2024, 24(8): 1210-1219. |
| [2] | 沈霞民, 熊涛, 李华, 沈璇. CLEFIA动态密码结构的零相关线性区分器构造研究[J]. 信息网络安全, 2024, 24(6): 948-958. |
| [3] | 赵耿, 马英杰, 董有恒. 混沌密码理论研究与应用新进展[J]. 信息网络安全, 2024, 24(2): 203-216. |
| [4] | 崔霆, 周屹东, 陈士伟, 张奕. 基于字的分组密码的谱值不变子空间[J]. 信息网络安全, 2024, 24(12): 1845-1854. |
| [5] | 张兴兰, 郭艳琨, 陈菲, 张丰. 基于量子Simon算法对分组密码类EM结构的密钥恢复攻击[J]. 信息网络安全, 2024, 24(1): 106-112. |
| [6] | 张兴兰, 张丰. 量子求解欧拉函数破解RSA算法[J]. 信息网络安全, 2023, 23(7): 1-8. |
| [7] | 张晓磊, 戴紫彬, 刘燕江, 曲彤洲. 面向分组密码的高速可重构模运算单元设计[J]. 信息网络安全, 2023, 23(5): 76-84. |
| [8] | 胡禹佳, 代政一, 孙兵. SIMON算法的差分—线性密码分析[J]. 信息网络安全, 2022, 22(9): 63-75. |
| [9] | 佟晓筠, 苏煜粤, 张淼, 王翥. 基于混沌和改进广义Feistel结构的轻量级密码算法[J]. 信息网络安全, 2022, 22(8): 8-18. |
| [10] | 杨云霄, 沈璇, 孙兵. Mysterion算法的不可能差分分析[J]. 信息网络安全, 2021, 21(8): 43-51. |
| [11] | 王建新, 周世强, 肖超恩, 张磊. 基于FPGA的FESH分组密码算法高速实现[J]. 信息网络安全, 2021, 21(1): 57-64. |
| [12] | 董晓丽, 商帅, 陈杰. 分组密码9轮Rijndael-192的不可能差分攻击[J]. 信息网络安全, 2020, 20(4): 40-46. |
| [13] | 向永谦, 宋智琪, 王天宇. 一种基于双明文的数据对称加密算法[J]. 信息网络安全, 2018, 18(7): 69-78. |
| [14] | 游伟青, 陈小明, 齐健. 一类抗量子计算的公钥密码算法研究[J]. 信息网络安全, 2017, 17(4): 53-60. |
| [15] | . 基于格的大数据动态存储完整性验证方案[J]. , 2014, 14(4): 46-. |
| 阅读次数 | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
全文 29
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
摘要 29
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||