基于量子Simon算法对分组密码类EM结构的密钥恢复攻击

doi:10.3969/j.issn.1671-1122.2024.01.010

信息网络安全 ›› 2024, Vol. 24 ›› Issue (1): 106-112.doi: 10.3969/j.issn.1671-1122.2024.01.010

基于量子Simon算法对分组密码类EM结构的密钥恢复攻击

张兴兰, 郭艳琨(), 陈菲, 张丰

北京工业大学信息学部，北京 100020

收稿日期:2023-06-25 出版日期:2024-01-10 发布日期:2024-01-24
通讯作者: 郭艳琨 E-mail:dimple_guo@emails.bjut.edu.cn
作者简介:张兴兰（1970—），女，山西，教授，博士，主要研究方向为密码和量子计算|郭艳琨（1998—），女，天津，硕士研究生，主要研究方向为对称密码和量子计算|陈菲（1999—），女，北京，硕士研究生，主要研究方向为量子密码|张丰（1998—），男，江西，硕士研究生，主要研究方向为量子机器学习
基金资助:
北京市自然科学基金(4212015)

Key Recovery Attacks on Block Cipher EM-Like Structures Based on Quantum Simon’s Algorithm

ZHANG Xinglan, GUO Yankun(), CHEN Fei, ZHANG Feng

Faculty of Information Technology, Beijing University of Technology, Beijing 100020, China

Received:2023-06-25 Online:2024-01-10 Published:2024-01-24
Contact: GUO Yankun E-mail:dimple_guo@emails.bjut.edu.cn

摘要/Abstract

摘要：

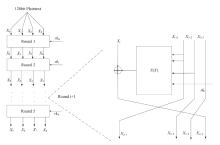
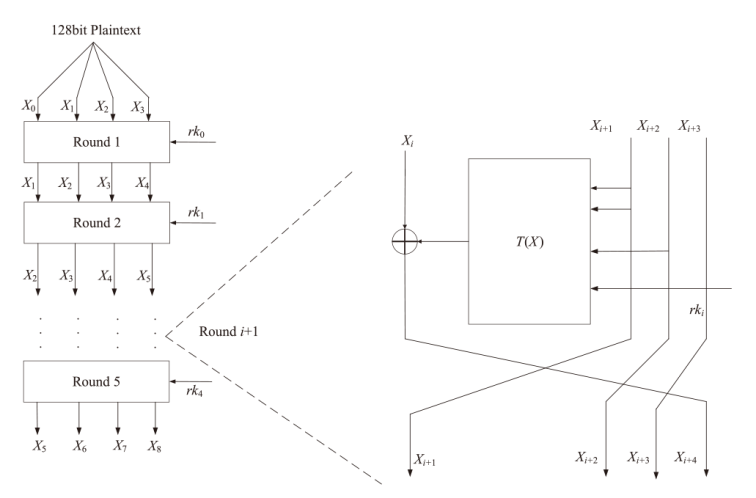
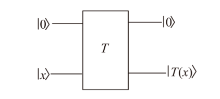
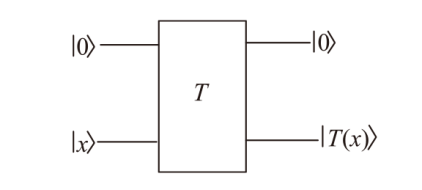
文章基于量子Simon算法（一类经典量子周期寻找算法）的量子过程以及应用，对类EM结构进行基于量子Simon算法的密码分析，以类EM结构的加密算法为研究对象，运用量子Simon算法，构造适用于Simon算法的函数，对类EM加密结构的5轮加密过程进行密钥恢复攻击。结果显示，在密钥长度的多项式时间内，文章所提方法可以成功恢复出第五轮加密密钥，且根据此密钥可以分析出其他轮密钥。研究结果表明，在密钥长度的多项式时间内，可以找到其中一个密钥，量子条件下密钥的可恢复性说明该结构的安全轮数应当高于5轮，为未来对称密码体制的研究和发展奠定了一定的基础。

关键词: 量子, 分组密码, Simon算法, 密钥恢复攻击

Abstract:

This paper studied the quantum process of Quantum Simon’s algorithm (one of classical quantum cycle finding algorithms) as well as its applications, and conducts cryptanalysis based on quantum Simon algorithm on EM-like structures, takes the encryption algorithm of EM-like structures as the object of research, applies quantum Simon algorithm, constructs the function applicable to Simon algorithm, and performs the key recovery attack on the 5-round encryption process of the encrypted structure of EM-like structures. The results show that the fifth round of encryption key can be successfully recovered in polynomial time of the key length, and other keys can be analyzed based on this key. The key recovery indicates that the quantum version of the structure is insecure, i.e., one of the keys can be found at polynomial time of the key length. It provides some basis for future research and development of symmetric cryptosystems.

Key words: quantum, block cipher, Simon’s algorithm, key recovery attack

中图分类号:

TP309

张兴兰, 郭艳琨, 陈菲, 张丰. 基于量子Simon算法对分组密码类EM结构的密钥恢复攻击[J]. 信息网络安全, 2024, 24(1): 106-112.

ZHANG Xinglan, GUO Yankun, CHEN Fei, ZHANG Feng. Key Recovery Attacks on Block Cipher EM-Like Structures Based on Quantum Simon’s Algorithm[J]. Netinfo Security, 2024, 24(1): 106-112.

图/表 4

参考文献 22

[1]	SHOR P. Algorithms for Quantum Computation: Discrete Logarithms and Factoring[C]// IEEE. 35th Annual Symposium on the Foundations of Computer Science. New York: IEEE, 1994: 124-134.
[2]	National Institute of Standards and Technology. Submission Requirements and Evaluation Criteria for the Post-Quantum Cryptography Standardization Process[EB/OL]. [2023-06-18]. https://csrc.nist.gov/CSRC/media/Projects/Post-Quantum-Cryptography/documents/call-for-proposals-final-dec-2016.pdf.
[3]	Grover L K. A Fast Quantum Mechanical Algorithm for Database Search[EB/OL]. (1996-11-19) [2023-06-18]. https://doi.org/10.48550/arXiv.quant-ph/9605043.
[4]	XIE Huiqin, YANG Li. A Quantum Related-Key Attack Based on the Bernstein-Vazirani Algorithm[EB/OL]. (2020-07-14) [2023-06-18]. https://link.springer.com/article/10.1007/s11128-020-02741-2.
[5]	KAPLAN M, LEURENT G, LEVERRIER A, et al. Quantum Differential and Linear Cryptanalysis[EB/OL]. (2017-05-07) [2023-06-18]. https://doi.org/10.48550/arXiv.1510.05836.
[6]	XIE Huiqin, YANG Li. Quantum Impossible Differential and Truncated Differential Cryptanalysis[EB/OL]. (2018-07-23) [2023-06-18]. https://doi.org/10.48550/arXiv.1712.06997.
[7]	VAZIRANI U. On the Power of Quantum Computation[J]. Philosophical Transactions Mathematical Physical & Engineering Sciences, 1998, 356(1743): 1759-1768.
[8]	KUWAKADO H, MORII M. Quantum Distinguisher between the 3-Round Feistel Cipher and the Random Permutation[C]// IEEE. IEEE International Symposium on Information Theory. New York: IEEE, 2010: 2682-2685.
[9]	KUWAKADO H, MORII M. Security on the Quantum-Type Even-Mansour Cipher[C]// IEEE. Information Theory and Its Applications (ISITA), 2012 International Symposium on. New York: IEEE, 2012: 312-316.
[10]	SANTOLI T, SCHAFFNER C. Using Simon's Algorithm to Attack Symmetric-Key Cryptographic Primitives[EB/OL]. (2017-01-31) [2023-06-18]. https://doi.org/10.48550/arXiv.1603.07856.
[11]	MALVIYA A K, TIWARI N, CHAWLA M. Quantum Cryptanalytic Attacks of Symmetric Ciphers: A Review[J]. Computers and Electrical Engineering, 2022: 101-109.
[12]	GUO Jian, JEAN J, NIKOLI I, et al. Extended Meet-in-the-Middle Attacks on Some Feistel Constructions[J]. Designs Codes and Cryptography, 2016, 80(3): 587-618. doi: 10.1007/s10623-015-0120-4 URL
[13]	PATARIN J. Generic Attacks on Feistel Schemes[C]// Springer. International Conference on the Theory and Application of Cryptology and Information Security. Heidelberg: Springer, 2001: 222-238.
[14]	KIM P, HAN D, JEONG K C. Time-Space Complexity of Quantum Search Algorithms in Symmetric Cryptanalysis: Applying to AES and SHA-2[J]. Quantum Information Processing, 2018, 17(12): 1-39. doi: 10.1007/s11128-017-1770-0 URL
[15]	DONG Xiaoyang, DONG Bingyou, WANG Xiaoyun. Quantum Attacks on Some Feistel Block Ciphers[J]. Designs, Codes and Cryptography. 2020(88): 1179-1203.
[16]	KAPLAN M, LEURENT G, LEVERRIER A, et al. Breaking Symmetric Cryptosystems Using Quantum Period Finding[C]// Springer. Annual International Cryptology Conference. Heidelberg: Springer, 2016: 207-237.
[17]	LEVERRIER A. Quantum Differential Cryptanalysis[EB/OL]. (2015-02-12) [2023-06-18]. http://www.dagstuhl.de/en/program/calendar/semhp/?semnr=15371.
[18]	BERNSTEIN E, VAZIRANI U. Quantum Complexity Theory[J]. Siam Journal on Computing, 1997, 26(5): 1411-1473. doi: 10.1137/S0097539796300921 URL
[19]	DAEMEN J, RIJMEN V. Probability Distributions of Correlation and Differentials in Block Ciphers[J]. Journal of Mathematical Cryptology, 2007, 1(3): 221-242.
[20]	KAPLAN M. Quantum Attacks Against Iterated Block Ciphers[J]. Matematicheskie Voprosy Kriptografii, 2014, 34: 71-90.
[21]	SHIMON E, YISHAY M. A Construction of a Cipher from a Single Pseudorandom Permutation[J]. Journal of Cryptology, 1997, 10(3): 151-161. doi: 10.1007/s001459900025 URL
[22]	KATZ J, LINDELL Y. Introduction to Modern Cryptography[M]. Boca Raton: Chapman & Hall/CRC, 2007.

基于量子Simon算法对分组密码类EM结构的密钥恢复攻击

Key Recovery Attacks on Block Cipher EM-Like Structures Based on Quantum Simon’s Algorithm

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 4

参考文献 22

相关文章 15

编辑推荐

Metrics

本文评价

[1]	李志慧, 罗双双, 韦性佳. 基于一类受限存取结构上的量子秘密共享方案[J]. 信息网络安全, 2023, 23(8): 32-40.
[2]	张兴兰, 张丰. 量子求解欧拉函数破解RSA算法[J]. 信息网络安全, 2023, 23(7): 1-8.
[3]	杨宇光, 卢嘉煜. 一种基于星型簇态的动态的分级的量子秘密共享协议[J]. 信息网络安全, 2023, 23(6): 34-42.
[4]	张晓磊, 戴紫彬, 刘燕江, 曲彤洲. 面向分组密码的高速可重构模运算单元设计[J]. 信息网络安全, 2023, 23(5): 76-84.
[5]	肖昊, 赵延睿, 胡越, 刘笑帆. 抗量子密码中快速数论变换的硬件设计与实现[J]. 信息网络安全, 2023, 23(4): 72-79.
[6]	刘兴斌, 刘聪. 基于级联混沌系统和量子Baker映射的图像加密算法[J]. 信息网络安全, 2023, 23(12): 49-58.
[7]	胡禹佳, 代政一, 孙兵. SIMON算法的差分—线性密码分析[J]. 信息网络安全, 2022, 22(9): 63-75.
[8]	佟晓筠, 苏煜粤, 张淼, 王翥. 基于混沌和改进广义Feistel结构的轻量级密码算法[J]. 信息网络安全, 2022, 22(8): 8-18.
[9]	贾恒越, 刘康婷, 武霞, 王卯宁. 基于Bell态的量子支票协议[J]. 信息网络安全, 2022, 22(6): 38-43.
[10]	陶云亭, 孔凡玉, 于佳, 徐秋亮. 抗量子格密码体制的快速数论变换算法研究综述[J]. 信息网络安全, 2021, 21(9): 46-51.
[11]	杨云霄, 沈璇, 孙兵. Mysterion算法的不可能差分分析[J]. 信息网络安全, 2021, 21(8): 43-51.
[12]	刘璐, 李志慧, 芦殿军, 闫晨红. 基于线性码的量子秘密共享方案[J]. 信息网络安全, 2021, 21(8): 62-69.
[13]	谢四江, 高琼, 冯雁. 基于可信中继量子密钥分发网络的最少公共节点多路径路由方案[J]. 信息网络安全, 2021, 21(7): 35-42.
[14]	李丹, 燕婷, 郭瑞. 基于交替量子漫步的量子彩色图像加密算法[J]. 信息网络安全, 2021, 21(6): 45-51.
[15]	周艺华, 董松寿, 杨宇光. 标准模型下基于格的身份代理部分盲签名方案[J]. 信息网络安全, 2021, 21(3): 37-43.