基于时间仓复用的高维量子密钥分发及应用

doi:10.3969/j.issn.1671-1122.2024.06.006

信息网络安全 ›› 2024, Vol. 24 ›› Issue (6): 879-892.doi: 10.3969/j.issn.1671-1122.2024.06.006

基于时间仓复用的高维量子密钥分发及应用

杨宇光¹(), 刘冰心¹, 徐光宝², 姜东焕³

1.北京工业大学信息学部,北京 100124
2.山东科技大学计算机科学与技术学院，青岛 266590
3.山东科技大学数学与系统科学学院，青岛 266590

收稿日期:2024-02-14 出版日期:2024-06-10 发布日期:2024-07-05
通讯作者: 杨宇光 yangyang7357@bjut.edu.cn
作者简介:杨宇光（1976—），女，河北，教授，博士，主要研究方向为量子计算和量子密码|刘冰心（1997—），女，山东，博士研究生，主要研究方向为量子通信和量子网络编码|徐光宝（1980—），男，山东，副教授，博士，主要研究方向为信息安全、密码学、区块链、图像处理、量子信息处理、量子密码、量子图像处理|姜东焕（1981—），女，山东，副教授，博士，主要研究方向为偏微分方程的图像处理、量子信息、量子密码、量子图像处理
基金资助:
国家自然科学基金(62071015);国家自然科学基金(62171264);山东省自然科学基金(ZR2023MF080)

High-Dimensional Quantum Key Distribution via Time-Bin Multiplexing and Applications

YANG Yuguang¹(), LIU Bingxin¹, XU Guangbao², JIANG Donghuan³

1. Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China
2. College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
3. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China

Received:2024-02-14 Online:2024-06-10 Published:2024-07-05

摘要/Abstract

摘要：

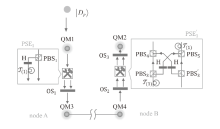
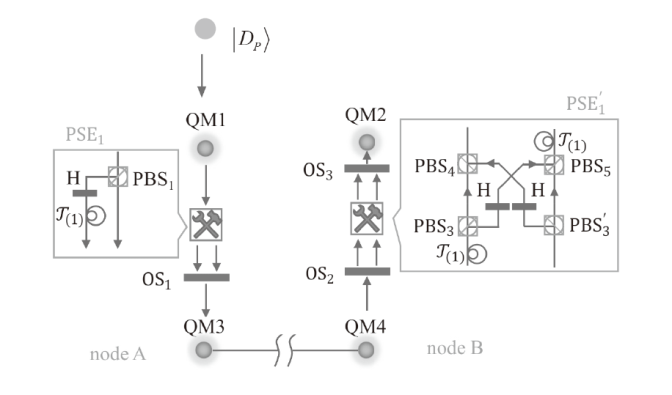
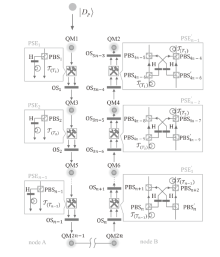
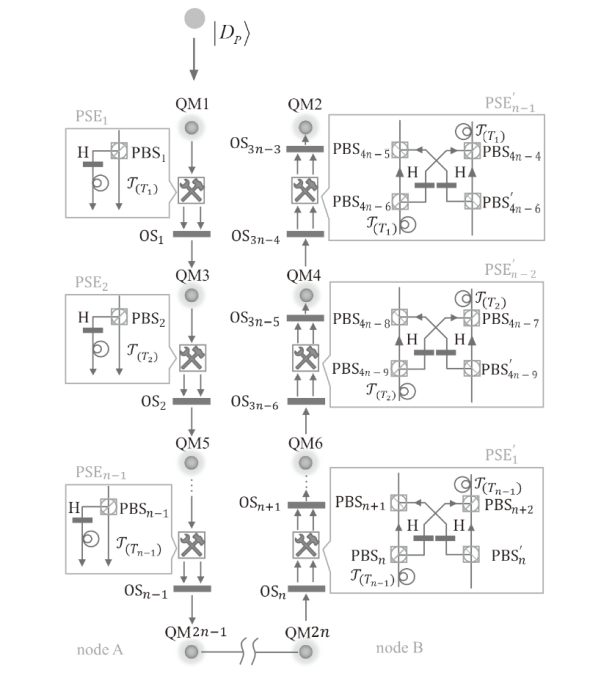
与二维量子密钥分发相比，高维量子密钥分发（High-Dimensional Quantum Key Distribution，HD-QKD）能够提供更高的密钥率并且可以容忍更多的噪声。然而，在量子通信中，对高维量子系统的操作限制了其实用性。文章基于时间仓复用提出了一种HD-QKD协议。首先，使用高维编码的单光子在通信双方的多对二维量子存储器（Quantum Memory，QM）之间创建可预报的并行纠缠；然后，通过对多对QM进行贝尔态测量，两个通信方可以检测窃听并获取密钥，无需额外的测量来检验安全性，这使得HD-QKD协议在成本和效率上都具有优势。此外，文章获得了实现最优密钥容量的条件，并讨论了HD-QKD协议的两个重要的密码学应用，即确定性安全的量子通信和量子保密查询。与现有方法相比，两者在效率上都有显著提高。综上所述，时间仓复用方法在解决密码学问题中具有强大能力。

关键词: 量子密钥分发, 时间仓复用, 高维编码

Abstract:

High-dimensional quantum key distribution (HD-QKD) can provide higher secret key rates and tolerate more noise than two-dimensional QKD. However, the manipulation of quantum systems of higher dimensions limits the practicality in quantum communications. This article presented an alternative protocol for HD-QKD based on time-bin multiplexing. Parallel entanglement was first created between multiple pairs of two-dimensional quantum memories (QMs) located as two communicating parties in a heralded way by means of single photons with high-dimensional encoding. Then by performing Bell state measurements on their QMs by twos, two communicating parties could detect eavesdropping and obtain the secret key. No alternative measurements were needed to check security. This made the present HD-QKD protocol cost-effective and efficient. Furthermore, this article obtained the condition that the optimal key capacity was achieved. This article also discussed two other important cryptographic applications based on the present HD-QKD protocol, deterministic secure quantum communication and quantum privacy query, where the significant increased in efficiency over the existing methods can be achieved. In summary, the time-bin multiplexing method has strong capabilities in solving cryptographic problems.

Key words: quantum key distribution, time-bin multiplexing, high-dimensional encoding

中图分类号:

TP309

杨宇光, 刘冰心, 徐光宝, 姜东焕. 基于时间仓复用的高维量子密钥分发及应用[J]. 信息网络安全, 2024, 24(6): 879-892.

YANG Yuguang, LIU Bingxin, XU Guangbao, JIANG Donghuan. High-Dimensional Quantum Key Distribution via Time-Bin Multiplexing and Applications[J]. Netinfo Security, 2024, 24(6): 879-892.

图/表 4

图1

图2

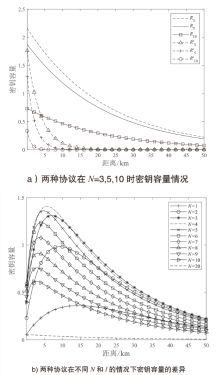
图3

图4

参考文献 74

[1]	EKERT A, RENNER R. The Ultimate Physical Limits of Privacy[J]. Nature, 2014, 507(7493): 443-447.
[2]	GISIN N, RIBORDY G, TITTEL W, et al. Quantum Cryptography[J]. Reviews of Modern Physics, 2002, 74(1): 145-195.
[3]	PIRANDOLA S, ANDERSEN U L, BANCHI L, et al. Advances in Quantum Cryptography[J]. Advances in Optics and Photonics, 2020, 12(4): 1012-1236.
[4]	BENNETT C H, BRASSARD G. Quantum Cryptography: Public Key Distribution and Coin Tossing[C]// IEEE. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing. New York: IEEE, 1984: 175-179.
[5]	EKERT A K. Quantum Cryptography Based on Bell’s Theorem[EB/OL]. (1991-08-05)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.67.661.
[6]	RALPH T C. Continuous Variable Quantum Cryptography[EB/OL]. (1999-12-08)[2024-02-12]. https://doi.org/10.1103/PhysRevA.61.010303.
[7]	HILLERY M. Quantum Cryptography with Squeezed States[EB/OL]. (2000-01-14)[2024-02-12]. https://doi.org/10.1103/PhysRevA.61.022309.
[8]	INOUE K, WAKS E, YAMAMOTO Y. Differential Phase Shift Quantum Key Distribution[EB/OL]. (2002-06-27)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.89.037902.
[9]	LO H K, CURTY M, QI B. Measurement-Device-Independent Quantum Key Distribution[EB/OL]. (2012-03-30)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.108.130503.
[10]	PIPARO N L, RAZAVI M, MUNRO W J. Measurement-Device-Independent Quantum Key Distribution with Nitrogen Vacancy Centers in Diamond[EB/OL]. (2017-02-27)[2024-02-12]. https://doi.org/10.1103/PhysRevA.95.022338.
[11]	ZHOU Yiheng, YU Zongwen, WANG Xiangbin. Making the Decoy-State Measurement-Device-Independent Quantum Key Distribution Practically Useful[EB/OL]. (2016-04-18)[2024-02-12]. https://doi.org/10.1103/PhysRevA.93.042324.
[12]	YIN Hualei, CHEN Tengyun, YU Zongwen, et al. Measurement-Device-Independent Quantum Key Distribution over a 404km Optical Fiber[EB/OL]. (2016-11-02)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.117.190501.
[13]	WANG Chao, SONG Xiaotian, YIN Zhenqiang, et al. Phase-Reference-Free Experiment of Measurement-Device-Independent Quantum Key Distribution[EB/OL]. (2015-12-15)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.115.160502.
[14]	ZHAO Yi, QI Bing, MA Xiongfeng, et al. Experimental Quantum Key Distribution with Decoy States[EB/OL]. (2006-02-22)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.96.070502.
[15]	LIAO Shengkai, CAI Wenqi, LIU Weiyue, et al. Satellite-to-Ground Quantum Key Distribution[J]. Nature, 2017, 549(7670): 43-47.
[16]	ZHU Haotao, HUANG Yizhi, LIU Hui, et al. Experimental Mode-Pairing Measurement-Device-Independent Quantum Key Distribution without Global Phase Locking[EB/OL]. (2023-01-17)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.130.030801.
[17]	LUCAMARINI M, YUAN Zhiliang, DYNES J F, et al. Overcoming the Rate-Distance Limit of Quantum Key Distribution without Quantum Repeaters[J]. Nature, 2018, 557(7705): 400-403.
[18]	WANG Rong, YIN Zhenqiang, LU Fengyu, et al. Optimized Protocol for Twin-Field Quantum Key Distribution[EB/OL]. (2020-08-28)[2024-02-12]. https://doi.org/10.1038/s42005-020-00415-0.
[19]	TENG Jun, YIN Zhenqiang, FANYUAN Guanjie, et al. Sending-or-not-Sending Twin-Field Quantum Key Distribution with Multiphoton States[EB/OL]. (2021-12-27)[2024-02-12]. https://doi.org/10.1103/PhysRevA.104.062441.
[20]	PIRANDOLA S, LAURENZA R, OTTAVIANI C, et al. Fundamental Limits of Repeaterless Quantum Communications[EB/OL]. (2017-04-26)[2024-02-12]. https://doi.org/10.1038/ncomms15043.
[21]	ERKILIÇ Ö, CONLON L, SHAJILAL B, et al. Surpassing the Repeaterless Bound with a Photon-Number Encoded Measurement-Device-Independent Quantum Key Distribution Protocol[EB/OL]. (2023-03-28)[2024-02-12]. https://doi.org/10.1038/s41534-023-00698-5.
[22]	TREIBER A, POPPE A, HENTSCHEL M, et al. A Fully Automated Entanglement-Based Quantum Cryptography System for Telecom Fiber Networks[EB/OL]. (2009-03-30)[2024-02-12]. https://doi.org/10.1088/1367-2630/11/4/045013.
[23]	ERHARD M, KRENN M, ZEILINGER A. Advances in High-Dimensional Quantum Entanglement[J]. Nature Reviews Physics, 2020, 2(7): 365-381.
[24]	HOWLAND G A, HOWELL J C. Efficient High-Dimensional Entanglement Imaging with a Compressive-Sensing Double-Pixel Camera[EB/OL]. (2013-02-20)[2024-02-12]. https://doi.org/10.1103/PhysRevX.3.011013.
[25]	HU Xiaomin, CHEN Jiangshan, LIU Biheng, et al. Experimental Test of Compatibility-Loophole-Free Contextuality with Spatially Separated Entangled Qutrits[EB/OL]. (2016-10-24)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.117.170403.
[26]	ZHANG Lijian, SILBERHORN C, WALMSLEY I A. Secure Quantum Key Distribution Using Continuous Variables of Single Photons[EB/OL]. (2008-03-18)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.100.110504.
[27]	ALI-KHAN I, BROADBENT C J, HOWELL J C. Large-Alphabet Quantum Key Distribution Using Energy-Time Entangled Bipartite States[EB/OL]. (2007-02-08)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.98.060503.
[28]	SHERIDAN L, SCARANI V. Security Proof for Quantum Key Distribution Using Qudit Systems[EB/OL]. (2010-09-07)[2024-02-12]. https://doi.org/10.1103/PhysRevA.82.030301.
[29]	SHERIDAN L, SCARANI V. Erratum: Security Proof for Quantum Key Distribution Using Qudit Systems[Phys. Rev. A 82, 030301 (R)( 2010)][EB/OL]. (2011-03-07)[2024-02-12]. https://doi.org/10.1103/PhysRevA.83.039901.
[30]	TITTEL W, BRENDEL J, ZBINDEN H, et al. Quantum Cryptography Using Entangled Photons in Energy-Time Bell States[EB/OL]. (2000-05-15)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.84.4737.
[31]	ALI-KHAN I, BROADBENT C J, HOWELL J C. Large-Alphabet Quantum Key Distribution Using Energy-Time Entangled Bipartite States[EB/OL]. (2007-02-08)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.98.060503.
[32]	ZHONG Tian, ZHOU Hongchao, HORANSKY R D, et al. Photon-Efficient Quantum Key Distribution Using Time-Energy Entanglement with High-Dimensional Encoding[EB/OL]. (2015-02-04)[2024-02-12]. https://doi.org/10.1088/1367-2630/17/2/022002.
[33]	ETCHEVERRY S, CAÑAS G, GÓMEZ E S, et al. Quantum Key Distribution Session with 16-Dimensional Photonic States[EB/OL]. (2013-07-30)[2024-02-12]. https://doi.org/10.1038/srep02316.
[34]	LI Dongdong, ZHAO Meisheng, LI Zhi, et al. High Dimensional Quantum Key Distribution with Temporal and Polarization Hybrid Encoding[EB/OL]. (2022-01-21)[2024-02-12]. https://doi.org/10.1016/j.yofte.2022.102828.
[35]	MAIR A, VAZIRI A, WEIHS G, et al. Entanglement of the Orbital Angular Momentum States of Photons[J]. Nature, 2001, 412(6844): 313-316.
[36]	MOLINA-TERRIZA G, VAZIRI A, ŘEHÁČEK J, et al. Triggered Qutrits for quantum Communication Protocols[EB/OL]. (2004-04-23)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.92.167903.
[37]	MAFU M, DUDLEY A, GOYAL S, et al. Higher-Dimensional Orbital-Angular-Momentum-Based Quantum Key Distribution with Mutually Unbiased Bases[EB/OL]. (2013-09-05)[2024-02-12]. https://doi.org/10.1103/PhysRevA.88.032305.
[38]	ISLAM N T, LIM C C W, CAHALL C, et al. Provably Secure and High-Rate Quantum Key Distribution with Time-Bin Qudits[EB/OL]. (2017-11-24)[2024-02-12]. https://doi.org/10.1126/sciadv.1701491.
[39]	VAGNILUCA I, DA L B, RUSCA D, et al. Efficient Time-Bin Encoding for Practical High-Dimensional Quantum Key Distribution[EB/OL]. (2020-07-17)[2024-02-12]. https://doi.org/10.1103/PhysRevApplied.14.014051.
[40]	PIPARO N L, MUNRO W J, NEMOTO K. Quantum Multiplexing[EB/OL]. (2019-02-27)[2024-02-12]. https://doi.org/10.1103/PhysRevA.99.022337.
[41]	XIE Zhihao, LIU Yijie, MO Xiang, et al. Quantum Entanglement Creation for Distant Quantum Memories via Time-Bin Multiplexing[EB/OL]. (2021-12-06)[2024-02-12]. https://doi.org/10.1103/PhysRevA.104.062409.
[42]	LIU Chenxu, DUTT M G, PEKKER D. Single-Photon Heralded Two-Qubit Unitary Gates for Pairs of Nitrogen-Vacancy Centers in Diamond[EB/OL]. (2018-11-27)[2024-02-12]. https://doi.org/10.1103/PhysRevA.98.052342.
[43]	CHILDRESS L, HANSON R. Diamond NV Centers for Quantum Computing and Quantum Networks[J]. MRS Bulletin, 2013, 38(2): 134-138.
[44]	BLOK M S, KALB N, REISERER A, et al. Towards Quantum Networks of Single Spins: Analysis of a Quantum Memory with an Optical Interface in Diamond[J]. Faraday Discussions, 2015, 184: 173-182. doi: 10.1039/c5fd00113g pmid: 26411802
[45]	DOHERTY M W, MANSON N B, DELANEY P, et al. The Nitrogen-Vacancy Colour Centre in Diamond[J]. Physics Reports, 2013, 528(1): 1-45.
[46]	XIE Yuanmei, LU Yushuo, WENG Chenxun, et al. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference[EB/OL]. (2022-04-21)[2024-02-12]. https://doi.org/10.1103/PRXQuantum.3.020315.
[47]	ZHOU Lai, LIN Jinping, XIE Yuanmei, et al. Experimental Quantum Communication Overcomes the Rate-Loss Limit without Global Phase Tracking[EB/OL]. (2023-06-20)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.130.250801.
[48]	ŻUKOWSKI M, ZEILINGER A, HORNE M A, et al. ‘‘Event-Ready-Detectors’’ Bell Experiment via Entanglement Swapping[EB/OL]. (1993-12-27)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.71.4287.
[49]	NING Yu, KANG Yihao, SHI Zhicheng, et al. Efficient Implementation of Complete and Nondestructive Bell-State Measurement for Trapped Ions with Reverse Engineering[EB/OL]. (2020-11-18)[2024-02-12]. https://doi.org/10.1088/1612-202X/abc32d.
[50]	WELTE S, THOMAS P, HARTUNG L, et al. A Nondestructive Bell-State Measurement on Two Distant Atomic Qubits[J]. Nature Photonics, 2021, 15(7): 504-509.
[51]	BARRETT S D, KOK P, NEMOTO K, et al. Symmetry Analyzer for Nondestructive Bell-State Detection Using Weak Nonlinearities[EB/OL]. (2005-06-07)[2024-02-12]. https://doi.org/10.1103/PhysRevA.71.060302.
[52]	REN Xifeng, GUO Guoping, GUO Guangcan. Complete Bell-States Analysis Using Hyper-Entanglement[J]. Physics Letters A, 2005, 343(1-3): 8-11.
[53]	LI Tao, MIRANOWICZ A, HU Xuedong, et al. Quantum Memory and Gates Using a Λ-Type Quantum Emitter Coupled to a Chiral Waveguide[EB/OL]. (2018-06-11)[2024-02-12]. https://doi.org/10.1103/PhysRevA.97.062318.
[54]	JIANG Dong, CHEN Yuanyuan, GU Xuemei, et al. Deterministic Secure Quantum Communication Using a Single d-Level System[EB/OL]. (2017-03-22)[2024-02-12]. https://doi.org/10.1038/srep44934.
[55]	YANG Yuguang, DONG Jingru, YANG Yongli, et al. High-Capacity Measurement-Device-Independent Deterministic Secure Quantum Communication[EB/OL]. (2021-06-05)[2024-02-12]. https://doi.org/10.1007/s11128-021-03129-6.
[56]	ROY S, MAITRA A, MUKHOPADHYAY S. Measurement-Device-Independent Quantum Private Query with Qutrits[EB/OL]. (2018-09-07)[2024-02-12]. https://doi.org/10.1142/S0219749918500454.
[57]	GAO Fei, LIU Bin, HUANG Wei, et al. Postprocessing of the Oblivious Key in Quantum Private Query[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2014, 21(3): 98-108.
[58]	GAO Fei, LIU Bin, WEN Qiaoyan, et al. Flexible Quantum Private Queries Based on Quantum Key Distribution[J]. Optics Express, 2012, 20(16): 17411-17420. doi: 10.1364/OE.20.017411 pmid: 23038294
[59]	WEI T C, BARREIRO J T, KWIAT P G. Hyperentangled Bell-State Analysis[EB/OL]. (2007-06-27)[2024-02-12]. https://doi.org/10.1103/PhysRevA.75.060305.
[60]	PISENTI N, GAEBLER C P E, LYNN T W. Distinguishability of Hyperentangled Bell States by Linear Evolution and Local Projective Measurement[EB/OL]. (2011-08-26)[2024-02-12]. https://doi.org/10.1103/PhysRevA.84.022340.
[61]	SHENG Yubo, DENG Fuguo, LONG Guilu. Complete Hyperentangled-Bell-State Analysis for Quantum Communication[EB/OL]. (2010-09-21)[2024-02-12]. https://doi.org/10.1103/PhysRevA.82.032318.
[62]	XIA Yan, CHEN Qingqin, SONG Jie, et al. Efficient Hyperentangled Greenberger-Horne-Zeilinger States Analysis with Cross-Kerr Nonlinearity[J]. Journal of the Optical Society of America B, 2012, 29: 1029-1037.
[63]	LI Xihan, GHOSE S. Self-Assisted Complete Maximally Hyperentangled State Analysis via the Cross-Kerr Nonlinearity[EB/OL]. (2016-02-01)[2024-02-12]. https://doi.org/10.1103/PhysRevA.93.022302.
[64]	LI Xihan, GHOSE S. Hyperentangled Bell-State Analysis and Hyperdense Coding Assisted by Auxiliary Entanglement[EB/OL]. (2017-08-21)[2024-02-12]. https://doi.org/10.1103/PhysRevA.96.020303.
[65]	JAKOBI M, SIMON C, GISIN N, et al. Practical Private Database Queries Based on a Quantum-Key-Distribution Protocol[EB/OL]. (2011-02-02)[2024-02-12]. https://doi.org/10.1103/PhysRevA.83.022301.
[66]	BORREGAARD J, PICHLER H, SCHRÖDER T, et al. One-Way Quantum Repeater Based on Near-Deterministic Photon-Emitter Interfaces[EB/OL]. (2020-06-30)[2024-02-12]. https://doi.org/10.1103/PhysRevX.10.021071.
[67]	DONOHUE J M, AGNEW M, LAVOIE J, et al. Coherent Ultrafast Measurement of Time-Bin Encoded Photons[EB/OL]. (2013-12-09)[2024-02-12]. https://doi.org/10.1103/PhysRevLett.111.153602.
[68]	REED G T, MASHANOVICH G, GARDES F Y, et al. Silicon Optical Modulators[J]. Nature Photonics, 2010, 4(8): 518-526.
[69]	WANG Cheng, ZHANG Mian, CHEN Xi, et al. Integrated Lithium Niobate Electro-Optic Modulators Operating at CMOS-Compatible Voltages[J]. Nature, 2018, 562(7725): 101-104.
[70]	BULUTA I, ASHHAB S, NORI F. Natural and Artificial Atoms for Quantum Computation[EB/OL]. (2011-09-19)[2024-02-12]. https://doi.org/10.1088/0034-4885/74/10/104401.
[71]	AWSCHALOM D D, HANSON R, WRACHTRUP J, et al. Quantum Technologies with Optically Interfaced Solid-State Spins[J]. Nature Photonics, 2018, 12(9): 516-527.
[72]	JANITZ E, BHASKAR M K, CHILDRESS L. Cavity Quantum Electrodynamics with Color Centers in Diamond[J]. Optica, 2020, 7(10): 1232-1252.
[73]	LÜTKENHAUS N, CALSAMIGLIA J, SUOMINEN K A. Bell Measurements for Teleportation[EB/OL]. (1999-05-01)[2024-02-12]. https://doi.org/10.1103/PhysRevA.59.3295.
[74]	HAQ S U, KHALIQUE A. Long Distance Cavity Entanglement by Entanglement Swapping Using Atomic Momenta[J]. Optics Communications, 2015, 334: 290-293.

基于时间仓复用的高维量子密钥分发及应用

High-Dimensional Quantum Key Distribution via Time-Bin Multiplexing and Applications

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 4

参考文献 74

相关文章 5

编辑推荐

Metrics

本文评价

[1]	白峻林, 尹华磊. 测量设备无关量子密钥分发中的改进型诱骗态方法[J]. 信息网络安全, 2024, 24(6): 926-936.
[2]	谢四江, 高琼, 冯雁. 基于可信中继量子密钥分发网络的最少公共节点多路径路由方案[J]. 信息网络安全, 2021, 21(7): 35-42.
[3]	冯雁, 刘念, 谢四江. 一种量子密钥池的双向使用方案[J]. 信息网络安全, 2020, 20(12): 40-46.
[4]	刘利娟, 李志慧, 支丹利. 可实现身份认证的多方量子密钥分发协议[J]. 信息网络安全, 2020, 20(11): 59-66.
[5]	黄鹏, 曾贵华. 连续变量量子密钥分发实际安全性研究进展[J]. 信息网络安全, 2017, 17(11): 7-12.