信息网络安全 ›› 2024, Vol. 24 ›› Issue (6): 893-902.doi: 10.3969/j.issn.1671-1122.2024.06.007
基于SM9标识密码算法的可否认环签名方案
丁勇1,2, 罗世东1,2, 杨昌松1,2( ), 梁海1,2
), 梁海1,2
- 1.桂林电子科技大学广西密码学与信息安全重点实验室,桂林 541004
2.桂林电子科技大学工业互联网安全与区块链广西工程研究中心,桂林 541004
-
收稿日期:2024-04-20出版日期:2024-06-10发布日期:2024-07-05 -
通讯作者:杨昌松csyang@guet.edu.cn -
作者简介:丁勇(1975—),男,重庆,教授,博士,CCF高级会员,主要研究方向为密码学及其应用、网络空间安全、人工智能、区块链及其应用|罗世东(1996—),男,江西,硕士研究生,主要研究方向为密码学及其应用|杨昌松(1989—),男,广西,副教授,博士,主要研究方向为云计算及其数据安全、应用密码学、网络安全、深度学习及其应用|梁海(1982—),男,广西,副教授,硕士,主要研究方向为区块链及其应用、网络安全、软件项目管理 -
基金资助:国家自然科学基金(62172119);国家自然科学基金(62362013);国家重点研发计划(2023YFB3107301);广西省自然科学基金(2024GXNSFAA010453);广西省自然科学基金(2024GXNSFDA010064)
An Identity-Based Deniable Ring Signature Scheme Based on SM9 Signature Algorithm
DING Yong1,2, LUO Shidong1,2, YANG Changsong1,2( ), LIANG Hai1,2
), LIANG Hai1,2
- 1. Guangxi Key Laboratory of Cryptography and Information Security, Guilin University of Electronic Technology, Guilin 541004, China
2. Guangxi Engineering Research Center of Industrial Internet Security and Blockchain, Guilin University of Electronic Technology, Guilin 541004, China
-
Received:2024-04-20Online:2024-06-10Published:2024-07-05
摘要:
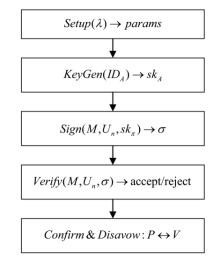
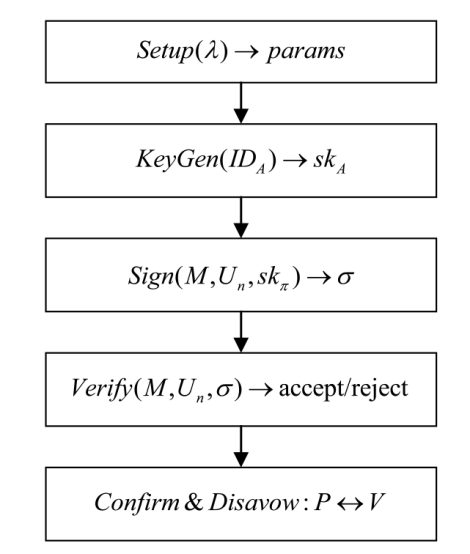
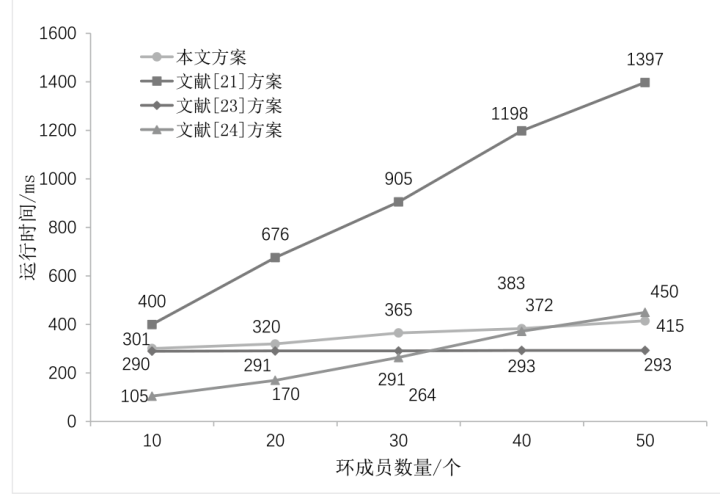
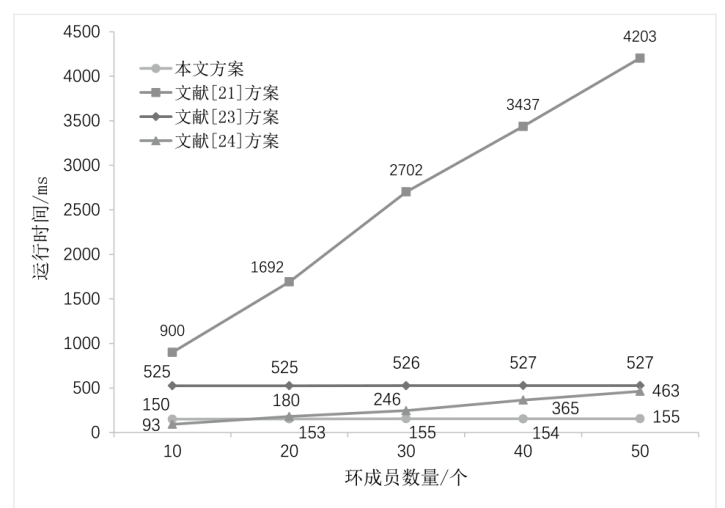
可否认环签名是环签名的拓展,允许环成员无需依赖可信第三方的情况下,能够在必要时通过特定协议确认或者否认自己的签名行为。可否认环签名具有追踪性,兼顾了隐私保护和可控监管的需求。将可否认环签名技术与基于标识的密码体系相结合,既能保留可否认环签名的主要特性,又能克服传统公钥基础设施下用户公钥和证书管理复杂的问题。文章基于SM9数字签名算法,提出一种身份标识的可否认环签名方案,能够实现对环签名的确认和否认,同时避免了公钥证书管理的问题。文章证明了所提方案在随机预言模型下满足正确性、不可伪造性、匿名性、可追踪性和不可诽谤性。通过模拟实验对通信和计算开销进行分析,所提方案仅需常数次的双线性配对操作,且在计算效率和通信成本方面均具有显著优势。
中图分类号:
引用本文
丁勇, 罗世东, 杨昌松, 梁海. 基于SM9标识密码算法的可否认环签名方案[J]. 信息网络安全, 2024, 24(6): 893-902.
DING Yong, LUO Shidong, YANG Changsong, LIANG Hai. An Identity-Based Deniable Ring Signature Scheme Based on SM9 Signature Algorithm[J]. Netinfo Security, 2024, 24(6): 893-902.
表1
符号说明
| 符号 | 说明 |
|---|---|
| p, N | 大素数 |
| $Z_{k}^{*}$ | 整数集合{1,2,…, k} |
| ${{G}_{1}}$,${{G}_{2}}$ | 加法循环群 |
| ${{G}_{T}}$ | 乘法循环群 |
| e | 双线性映射 |
| ${{P}_{1}}$,${{P}_{2}}$ | 分别是群${{G}_{1}}$和${{G}_{2}}$的生成元 |
| $H\left( * \right)$ | 哈希运算 |
| ${{P}_{pub-s}}$ | 签名主公钥 |
| $I{{D}_{i}}$ | 用户身份标识 |
| ${{U}_{n}}$ | 用户身份标识集合 |
| M, σ | 消息及其签名值 |
| [a]P | 群中的乘法:P的a倍点 |
| $\alpha ||\beta $ | $\alpha $与$\beta $拼接 |
| [1] | RIVEST R L, SHAMIR A, TAUMAN Y. How to Leak a Secret[C]// Springer. Advances in Cryptology—ASIACRYPT 2001: 7th International Conference on the Theory and Application of Cryptology and Information Security Gold Coast. Heidelberg: Springer, 2001: 552-565. |
| [2] | QIU Chi, ZHANG Shibin, CHANG Yan, et al. Electronic Voting Scheme Based on a Quantum Ring Signature[J]. International Journal of Theoretical Physics, 2021, 60: 1550-1555. |
| [3] | KOMANO Y, OHTA K, SHIMBO A, et al. Toward the Fair Anonymous Signatures: Deniable Ring Signatures[C]// Springer. Cryptographers’ Track at the RSA Conference. Heidelberg: Springer, 2006: 174-191. |
| [4] | WU Qianhong, SUSILO W, MU Yi, et al. Ad Hoc Group Signatures[C]// Springer. International Workshop on Security. Heidelberg: Springer, 2006: 120-135. |
| [5] | CAMENISCH J, MICHELS M. A Group Signature Scheme Based on an RSA-Variant[J]. BRICS Report Series, 1998, 5(27): 160-174. |
| [6] | BENALOH J, DE M M. One-Way Accumulators: A Decentralized Alternative to Digital Signatures[C]// Springer. Workshop on the Theory and Application of Cryptographic Techniques. Heidelberg: Springer, 1993: 274-285. |
| [7] | LIU D Y W, LIU J K, MU Yi, et al. Revocable Ring Signature[J]. Journal of Computer Science and Technology, 2007, 22: 785-794. |
| [8] | ZENG Shengke, JIANG Shaoquan, QIN Zhiguang. An Efficient Conditionally Anonymous Ring Signature in the Random Oracle Model[J]. Theoretical Computer Science, 2012, 461: 106-114. |
| [9] | ZENG Shengke, LI Qinyi, QIN Zhiguang, et al. Non-Interactive Deniable Ring Signature without Random Oracles[J]. Security and Communication Networks, 2016, 9(12): 1810-1819. |
| [10] | GAO Wen, CHEN Liqun, HU Yupu, et al. Lattice-Based Deniable Ring Signatures[J]. International Journal of Information Security, 2019, 18: 355-370. |
| [11] | PARK S, SEALFON A. It Wasn’t Me! Repudiability and Claimability of Ring Signatures[C]// Springer. Advances in Cryptology-CRYPTO 2019: 39th Annual International Cryptology Conference. Heidelberg: Springer, 2019: 159-190. |
| [12] | JIA Huiwen, TANG Chunming, ZHANG Yanhua. Lattice-Based Logarithmic-Size Non-Interactive Deniable Ring Signatures[J]. Entropy, 2021, 23(8): 980. |
| [13] | LIN Hao, WANG Mingqiang. Repudiable Ring Signature: Stronger Security and Logarithmic-Size[EB/OL]. (2022-03-01)[2024-04-15]. https://api.semanticscholar.org/CorpusID:207988596. |
| [14] | SHAMIR A. Identity-Based Cryptosystems and Signature Schemes[C]// Springer. Advances in Cryptology:Proceedings of CRYPTO 84 4. Heidelberg: Springer, 1985: 47-53. |
| [15] | ZHANG Fangguo, KIM K. ID-Based Blind Signature and Ring Signature from Pairings[C]// Springer. Advances in Cryptology-ASIACRYPT 2002. Heidelberg: Springer, 2002: 533-547. |
| [16] | LIN C Y, WU T C. An Identity-Based Ring Signature Scheme from Bilinear Pairings[C]// IEEE. 18th International Conference on Advanced Information Networking and Applications. New York: IEEE, 2004: 182-185. |
| [17] | CHOW S S M, YIU S M, HUI L C K. Efficient Identity Based Ring Signature[C]// Springer. Applied Cryptography and Network Security. Heidelberg: Springer, 2005: 499-512. |
| [18] | AU M H, LIU J K, SUSILO W, et al. Constant-Size ID-Based Linkable and Revocable-iff-Linked Ring Signature[C]// Springer. Progress in Cryptology-INDOCRYPT 2006. Heidelberg: Springer, 2006: 364-378. |
| [19] | XIE Zongxiao, DONG Kunxiang, ZHEN Jie. International Standardization of Domestic Commercial Cryptographic Algorithms and Their Corresponding Relations[J]. China Quality and Standards Review, 2021(5): 20-23, 29. |
| 谢宗晓, 董坤祥, 甄杰. 国产商用密码算法的国际标准化及其对应关系[J]. 中国质量与标准导报, 2021(5): 20-23,29. | |
| [20] | FAN Qing, HE Debiao, LUO Min, et al. Ring Signature Schemes Based on SM2 Digital Signature Algorithm[J]. Journal of Cryptologic Research, 2021, 8(4): 710-723. |
| 范青, 何德彪, 罗敏, 等. 基于SM2数字签名算法的环签名方案[J]. 密码学报, 2021, 8(4):710-723. | |
| [21] | PENG Cong, HE Debiao, LUO Min, et al. An Identity-Based Ring Signature Scheme for SM9 Algorithm[J]. Journal of Cryptologic Research, 2021, 8(4): 724-734. |
| 彭聪, 何德彪, 罗敏, 等. 基于SM9标识密码算法的环签名方案[J]. 密码学报, 2021, 8(4):724-734. | |
| [22] |
RAO Jintao, CUI Zhe. Secure E-Voting Protocol Based on SM9 Blind Signature and Ring Signature[J]. Computer Engineering, 2023, 49(6): 13-23, 33.
doi: 10.19678/j.issn.1000-3428.0066576 |
|
饶金涛, 崔喆. 基于SM9盲签名与环签名的安全电子选举协议[J]. 计算机工程, 2023, 49(6):13-23,33.
doi: 10.19678/j.issn.1000-3428.0066576 |
|
| [23] | AN Haoyang, HE Debiao, BAO Zijian, et al. Ring Signature Based on the SM9 Digital Signature and Its Application in Blockchain Privacy Protection[J]. Journal of Computer Research and Development, 2023, 60(11): 2545-2554. |
| 安浩杨, 何德彪, 包子健, 等. 基于SM9数字签名的环签名及其在区块链隐私保护中的应用[J]. 计算机研究与发展, 2023, 60(11):2545-2554. | |
| [24] | BAO Zijian, HE Debiao, PENG Cong, et al. Deniable Ring Signature Scheme Based on SM2 Digital Signature Algorithm[J]. Journal of Cryptologic Research, 2023, 10(2): 264-275. |
| 包子健, 何德彪, 彭聪, 等. 基于SM2数字签名算法的可否认环签名[J]. 密码学报, 2023, 10(2):264-275. | |
| [25] | HERRANZ J, SÁEZ G. Forking Lemmas for Ring Signature Schemes[C]// Springer. International Conference on Cryptology. Heidelberg: Springer, 2003: 266-279. |
| [26] | BARRETO P S L M, LIBERT B, MCCULLAGH N, et al. Efficient and Provably-Secure Identity-Based Signatures and Signcryption from Bilinear Maps[C]// Springer. Advances in Cryptology-ASIACRYPT 2005. Heidelberg: Springer, 2005: 515-532. |
| [27] | PEREIRA G C C F, SIMPLÍCIO J M A, NAEHRIG M, et al. A Family of Implementation-Friendly BN Elliptic Curves[J]. Journal of Systems and Software, 2011, 84(8): 1319-1326. |
| [1] | 欧阳梦迪, 孙钦硕, 李发根. SM9加密算法的颠覆攻击与改进[J]. 信息网络安全, 2024, 24(6): 831-842. |
| [2] | 张雪锋, 陈婷婷, 苗美霞, 程叶霞. 基于SM9的多接收者混沌密钥生成方案[J]. 信息网络安全, 2024, 24(4): 555-563. |
| [3] | 张艳硕, 袁煜淇, 李丽秋, 杨亚涛, 秦晓宏. 基于SM2的周期性可否认环签名方案[J]. 信息网络安全, 2024, 24(4): 564-573. |
| [4] | 翟鹏, 何泾沙, 张昱. 物联网环境下基于SM9算法和区块链技术的身份认证方法[J]. 信息网络安全, 2024, 24(2): 179-187. |
| [5] | 朱郭诚, 何德彪, 安浩杨, 彭聪. 基于区块链和SM9数字签名的代理投票方案[J]. 信息网络安全, 2024, 24(1): 36-47. |
| [6] | 周权, 陈民辉, 卫凯俊, 郑玉龙. 基于SM9的属性加密的区块链访问控制方案[J]. 信息网络安全, 2023, 23(9): 37-46. |
| [7] | 安浩杨, 何德彪, 包子健, 彭聪. 一种基于证书的数字签名方案[J]. 信息网络安全, 2023, 23(3): 13-21. |
| [8] | 张雪锋, 胡奕秀. 一种基于SM9的可撤销标识广播加密方案[J]. 信息网络安全, 2023, 23(1): 28-35. |
| [9] | 王圣雯, 胡爱群. 基于SM9算法的邮件加密系统设计[J]. 信息网络安全, 2022, 22(6): 53-60. |
| [10] | 吴克河, 程瑞, 郑碧煌, 崔文超. 电力物联网安全通信协议研究[J]. 信息网络安全, 2021, 21(9): 8-15. |
| [11] | 张昱, 孙光民, 李煜. 基于SM9算法的移动互联网身份认证方案研究[J]. 信息网络安全, 2021, 21(4): 1-9. |
| [12] | 周艺华, 吕竹青, 杨宇光, 侍伟敏. 基于区块链技术的数据存证管理系统[J]. 信息网络安全, 2019, 19(8): 8-14. |
| [13] | 张雪锋, 彭华. 一种基于SM9算法的盲签名方案研究[J]. 信息网络安全, 2019, 19(8): 61-67. |
| [14] | 俞惠芳, 高新哲. 多源网络编码同态环签名方案研究[J]. 信息网络安全, 2019, 19(2): 36-42. |
| [15] | 黎琳, 张旭霞. zk-snark的双线性对的国密化方案[J]. 信息网络安全, 2019, 19(10): 10-15. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||