面向分组密码的高速可重构模运算单元设计

doi:10.3969/j.issn.1671-1122.2023.05.008

摘要/Abstract

摘要：

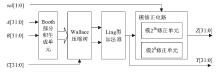
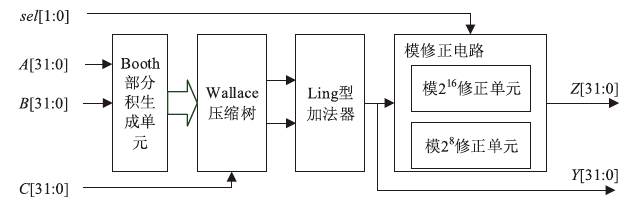
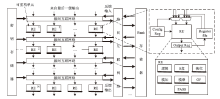
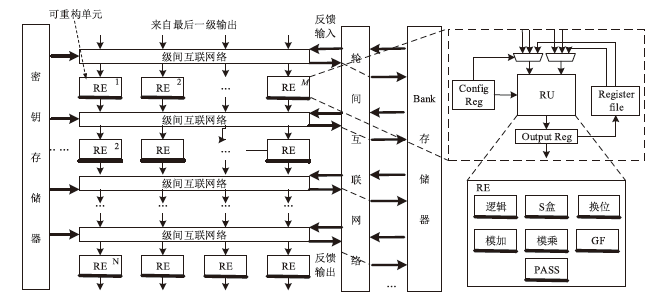
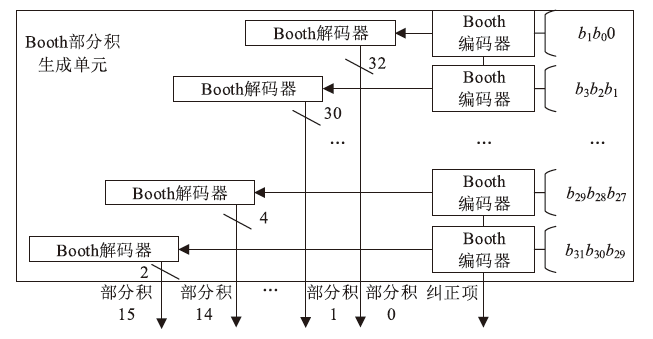
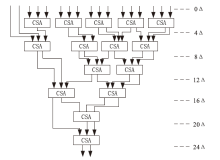
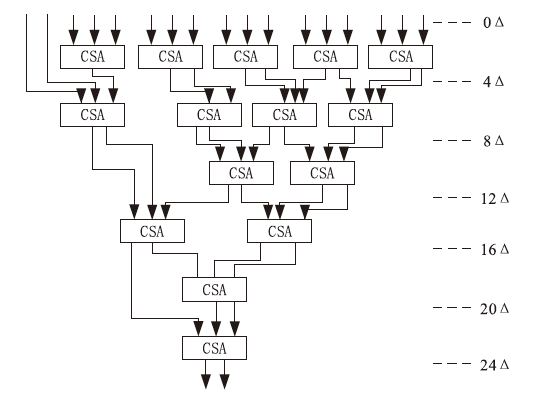
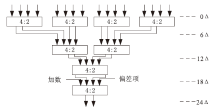
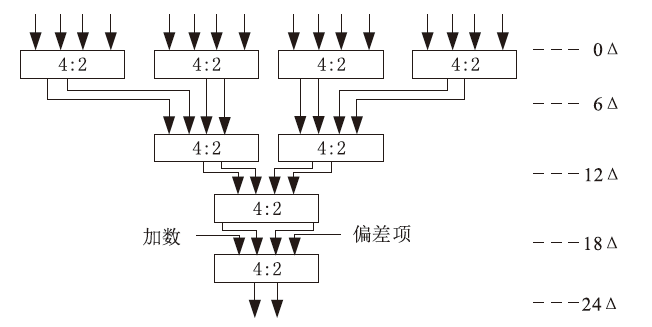
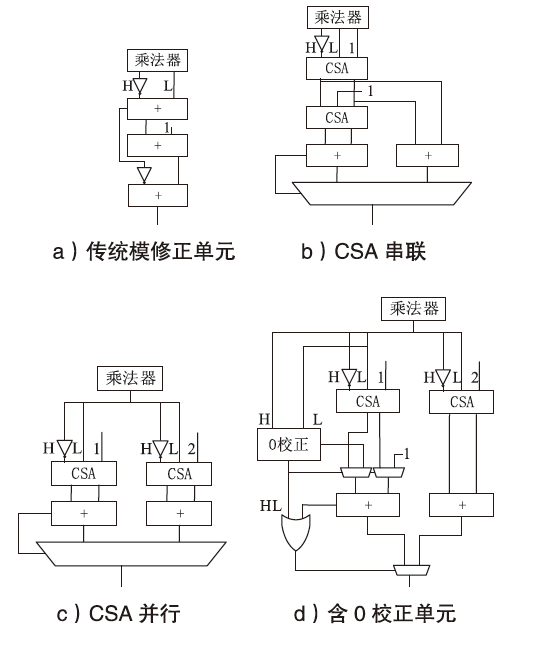
模运算单元是粗粒度可重构密码阵列（Coarse Grain Reconfigurable Cryptographic Array，CGRCA）的关键部件，通过重构不同处理位宽和模数的算术类密码算子来覆盖更多类型的分组密码，然而现有的模运算单元的执行延迟高且功能覆盖率低，限制了CGRCA整体性能的提升。文章通过分析分组密码模运算特性，提出一种可重构模运算方法，统一了该类算子的数学表达方式，并设计了一种可重构模运算单元（Reconfigurable Modulo Arithmetic Unit，RMAU），该单元支持5种模乘运算、3种模加运算和3种乘法累加运算。同时，通过舍弃部分积中的无用比特位、扩展Wallace树压缩求和过程、精简模修正电路执行路径，降低了该单元的关键路径延迟。基于CMOS 180 nm工艺测试了RMAU的功能与性能，实验结果表明，文章所提的RMAU具备高功能覆盖率，与模乘RCE单元、可扩展模乘结构和RNS乘法器相比，计算延迟分别降低了39%、44%和47%。

关键词: 可重构计算, 模乘运算, 分组密码, 模修正运算

Abstract:

Modulo arithmetic unit is the key component of coarse grain reconfigurable cryptographic array (CGRCA). It can cover more types of block ciphers by reconfiguring arithmetic cryptographic operators with different processing width and modulus. However, the high execution latency and low functional coverage of the existing modulo arithmetic units limit the overall performance improvement of CGRCA. By analyzing the characteristics of modulo arithmetic in block ciphers, this paper proposed reconfigurable modular arithmetic unit (RMAU), which unified the mathematical expression of the operators and designed a RMAU. The unit supported five modular multiplication operations, three modular addition operations, and three multiply-accumulate operations. At the same time, the critical path delay of the unit was optimized by discarding useless bits in the partial product, extending the Wallace tree to compress the summing process, and shortening the modular correction module’s execution path. The function and performance of RMAU were tested in CMOS 180 nm process. The experimental results show that while RMAU has high functional coverage, compared with modular multiplier RCE unit, extensible modular multiplier structure and RNS multiplier, the computation delay is reduced by 39%, 44% and 47%, respectively.

Key words: reconfigurable computing, modular multiplication, block cipher, modulo correction operation

中图分类号:

TP309

张晓磊, 戴紫彬, 刘燕江, 曲彤洲. 面向分组密码的高速可重构模运算单元设计[J]. 信息网络安全, 2023, 23(5): 76-84.

ZHANG Xiaolei, DAI Zibin, LIU Yanjiang, QU Tongzhou. Design of High Speed Reconfigurable Modulo Arithmetic Unit for Block Cipher[J]. Netinfo Security, 2023, 23(5): 76-84.

图/表 11

表1

图1

图2

图3

表2

图4

图5

图6

图7

图8

表3

参考文献 21

[1]	YUAN Hang. Research on Key Technologies of Dynamic Reconfigurable Cryptography Chip[D]. Beijing: Tsinghua University, 2019.
	袁航. 动态可重构密码芯片关键技术研究[D]. 北京: 清华大学, 2019.
[2]	MENG Tao, DAI Zibin. Research on Reconfigurable Modulo Operation Unit[J]. Computer Engineering, 2008, 34(6): 145-147. doi: 10.1108/EC-11-2015-0334 URL
	孟涛, 戴紫彬. 可重构模运算单元的研究[J]. 计算机工程, 2008, 34(6): 145-147.
[3]	LI Wei, DAI Zibin, CHEN Tao. Low-Power 32-bit Multiplier Based on Leapfrog Wallace Tree[J]. Computer Engineering, 2008, 34(17): 229-231.
	李伟, 戴紫彬, 陈韬. 基于跳跃式Wallace树的低功耗32位乘法器[J]. 计算机工程, 2008, 34(17): 229-231.
[4]	LI Wei, DAI Zibin, MENG Tao, et al. Design and Implementation of a High-Speed Reconfigurable Multiplier[EB/OL]. (2007-10-22)[2022-11-03]. https://ieeexplore.ieee.org/document/4415596.
[5]	JUANG T B, KUO C T, WU G L, et al. Multifunction RNS Modulo 2ⁿ ± 1 Multipliers[EB/OL]. (2021-09-06)[2022-11-03]. https://www.worldscientific.com/doi/abs/10.1142/S0218126612500272.
[6]	ZIMMERMANN R. Efficient VLSI Implementation of Modulo (2/Sup n//SPL Plusmn/1) Addition and Multiplication[EB/OL]. (1999-04-14)[2022-11-03]. https://ieeexplore.ieee.org/document/762841.
[7]	YAN Bin, LI Jun. Modulo 2n + 1 Multiplier Based on Radix-4 Booth Encoding[J]. Communications Technology, 2015, 48(10): 1168-1173.
	鄢斌, 李军. 基于Radix-4 Booth编码的模2n+1乘法器设计[J]. 通信技术, 2015, 48(10): 1168-1173.
[8]	VASSALOS E, BAKALIS D, VERGOS H T. Configurable Booth-Encoded Modulo 2(exp n)± 1 Multipliers[EB/OL]. (2012-06-12)[2022-11-03]. https://ieeexplore.ieee.org/document/6226138?tp=&arnumber=6226138.
[9]	MURALIDHARAN R, CHANG C H. Radix-4 and Radix-8 Booth Encoded Multi-Modulus Multipliers[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(11): 2940-2952. doi: 10.1109/TCSI.2013.2252642 URL
[10]	CHENG Bin, WANG Dongyan, HAN Xiansheng, et al. Research of the Nature of Cyclic Shift XOR in Cryptography[J]. Cyber Security and Data Governance, 2011, 30(11): 79-80.
	成彬, 王冬艳, 韩宪生, 等. 密码算法中的循环移位“异或”运算实质性研究[J]. 微型机与应用, 2011, 30(11): 79-80.
[11]	ZHANG Yan. Research and Design of RISC Architecture Specific Instruction Cryptographic Processor[D]. Zhengzhou: PLA Information Engineering University, 2008.
	张琰. RISC结构专用指令密码处理器研究与设计[D]. 郑州: 解放军信息工程大学, 2008.
[12]	XUE Yuqian, DAI Zibin. Reconfiurable Multi-Launch Pipeline Processing Architecture for Block Cipher[J]. Application of Electronic Technique, 2020, 46(4): 40-44.
	薛煜骞, 戴紫彬. 可重构分组密码多发射流水处理架构研究与设计[J]. 电子技术应用, 2020, 46(4): 40-44.
[13]	YEH W C, JEN C W. High-Speed Booth Encoded Parallel Multiplier Design[J]. IEEE Transactions on Computers, 2000, 49(7): 692-701. doi: 10.1109/12.863039 URL
[14]	FRIED R. Minimizing Energy Dissipation in High-Speed Multipliers[C]// ACM. Proceedings of 1997 International Symposium on Low Power Electronics and Design. New York: ACM, 1997: 214-219.
[15]	ZHAO Zhongmin, LIN Zhenghao. Design of an Improved Wallace Tree Multiplier[J]. Electronic Design & Application World-Nikkei Electronics China, 2006(8): 113-116.
	赵忠民, 林正浩. 一种改进的Wallace树型乘法器的设计[J]. 电子设计应用, 2006(8): 113-116.
[16]	KOREN I. Computer Arithmetic Algorithms[M]. Boston: Prentice-Hall, 1993.
[17]	CURIGER A V, BONNENBERG H, KAESLIN H. Regular VLSI Architectures for Multiplication Modulo (2/Sup n/+1)[J]. IEEE Journal of Solid-State Circuits, 1991, 26(7): 990-994. doi: 10.1109/4.92018 URL
[18]	LAI Xuejia, MASSEY J L. A Proposal for a New Block Encryption Standard[C]// Springer. Advances in Cryptology-EUROCRYPT’90. Berlin:Springer, 2001: 389-404.
[19]	YANG Xiaohui. Research on Reconfigurable Design Technology for Block Cipher Processing[D]. Zhengzhou: PLA Information Engineering University, 2007.
	杨晓辉. 面向分组密码处理的可重构设计技术研究[D]. 郑州: 解放军信息工程大学, 2007.
[20]	LI Jun, LYU Yongqi, Reconfigurable Design and Implementation of Modulo Multiplication[J]. Information Security And Communications Privacy, 2008(2): 97-99.
	李军, 吕永其. 模2ⁿ±1乘法的可重构设计与实现[J]. 信息安全与通信保密, 2008(2): 97-99.
[21]	LI Xiaoquan. Optimization and Design of Reconfigurable Array Processing Unit for Group Encryption Algorithm[D]. Nanjing: Southeast University, 2016.
	李小泉. 面向分组加密算法的可重构阵列处理单元优化与设计[D]. 南京: 东南大学, 2016.

模运算类型	模数	算法	算法数量
模加运算	2⁸	SAFER K、SAFER+、FEAL、HIGHT	4
	2¹⁶	IDEA、RC2、SAFER++	3
	2³²	Blowfish、MARS、CAST-128、CAST-256、GOST、WAKE、WiderWake、RC5、RC6、Twofish	10
模乘运算	2¹⁶	MESH	1
	2³²	MARS、RC6、E2、Twofish、Serpent、MultiSwap、Cipherunicorn-A	7
	2¹⁶+1	IDEA	1
	2³²-1	MMB	1

X₂_i₊₁	X₂_i	X₂_i_-1	X1b	X2b	Neg
0	0	0	1	1	0
0	0	1	0	1	0
0	1	0	0	1	0
0	1	1	1	0	0
1	0	0	1	0	1
1	0	1	0	1	1
1	1	0	0	1	1
1	1	1	1	1	1

乘法器	延迟/ns	面积/μm²	功耗-延迟积/ （ns·μm²）	工艺/nm	支持算法
模乘RCE单元^[19]	4.62	127260	587941	180	模2¹⁶乘法、模2¹⁶+1乘法、模2³²乘法、模2³²-1乘法
高速可重构乘法器^[4]	2.80	182752	511705.6	180	16 bit乘法、32 bit乘法、模2¹⁶乘法、模2¹⁶+1乘法
可扩展模乘结构^[20]	5.00	-	-	180	32 bit乘法、模2¹⁶+1乘法、模2³²+1乘法
PE阵列^[21]	1.27	1585	2012.95	40	模2⁸加法、模2¹⁶加法、模2³²加法
RNS乘法器^[5]	5.28	61661	325570.08	180	模2¹⁶+1乘法、模2¹⁶-1乘法
RMAU	1.17	11778	13780.26	40	模2⁸乘法、模2¹⁶乘法、模2³²乘法、8比特乘法、16比特乘法模2⁸加法、模2¹⁶加法、模2³²加法模2⁸乘法、模2¹⁶乘法、模2³²乘法模2¹⁶+1乘法、模2³²+1乘法、乘法累加运算
RMAU	2.80	86765	242942	180