密钥管理服务系统下的多方协同SM4加/解密方案

doi:10.3969/j.issn.1671-1122.2021.08.003

信息网络安全 ›› 2021, Vol. 21 ›› Issue (8): 17-25.doi: 10.3969/j.issn.1671-1122.2021.08.003

密钥管理服务系统下的多方协同SM4加/解密方案

杨伊¹, 何德彪¹(), 文义红², 罗敏¹

1.武汉大学国家网络安全学院,武汉 430072
2.中国电子科技集团有限公司第五十四研究所,石家庄 050000

收稿日期:2021-05-11 出版日期:2021-08-10 发布日期:2021-09-01
通讯作者: 何德彪 E-mail:hedebiao@163.com
作者简介:杨伊（1993—）,女,湖北,博士研究生,主要研究方向为数字签名和安全多方计算|何德彪（1980—）,男,湖北,教授,博士,主要研究方向为密码协议、信息安全、区块链技术与应用|文义红（1977—）,男,湖北,高级工程师,博士,主要研究方向为航天区块链、模拟仿真训练|罗敏（1974—）,男,湖北,副教授,博士,主要研究方向为密码协议、信息安全、区块链技术与应用
基金资助:
国家重点研发计划(2018YFC1604000);国家自然科学基金(61932016);国家自然科学基金(61972294)

Multi-party Collaborative SM4 Encryption/Decryption Scheme in Key Management Service

YANG Yi¹, HE Debiao¹(), WEN Yihong², LUO Min¹

1. School of Cyber Science and Engineering, Wuhan University, Wuhan 430072, China
2. The 54th Research Institute of CETC, Shijiazhuang 050000, China

Received:2021-05-11 Online:2021-08-10 Published:2021-09-01
Contact: HE Debiao E-mail:hedebiao@163.com

摘要/Abstract

摘要：

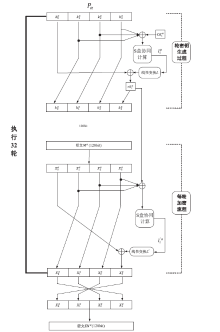
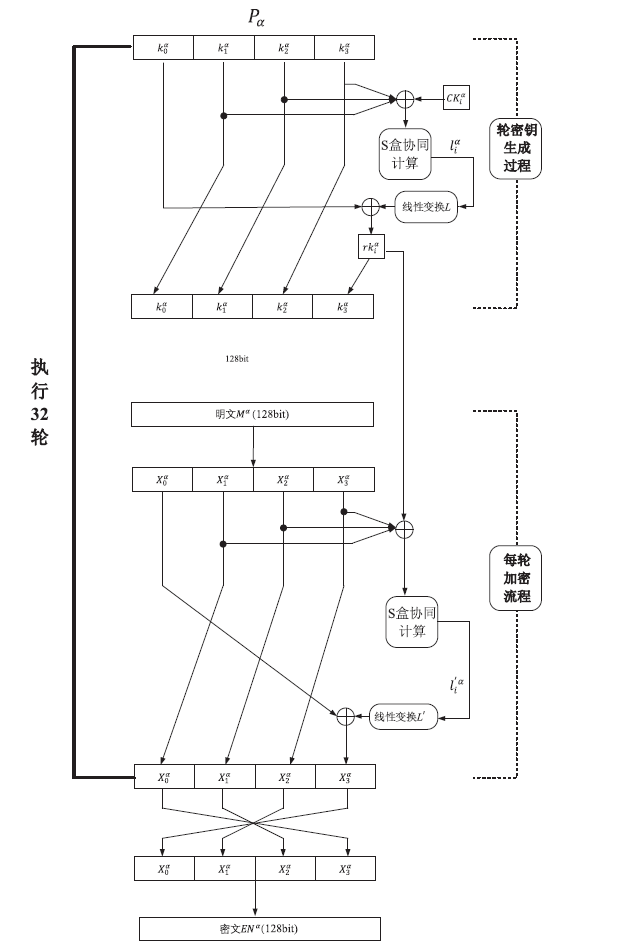
随着密码国产化与密钥保护需求的不断增加,商用密码算法与密钥安全管理的复合应用成为专家和学者关注的焦点之一。为解决加 / 解密方案中私钥易泄露的问题,针对密钥管理服务系统,文章提出一种安全高效的多方协同SM4加/ 解密方案。该方案利用一次一密且可以预计算的Beaver乘法三元组构成安全两方乘加转换器,保证多方S盒协同计算,从而实现安全高效的多方协同SM4加/解密,有效降低了在线交互过程中的计算开销与通信开销。安全性分析表明,文章方案在恶意模型下是安全的;其他性能分析详细统计了方案的计算开销与通信开销,表明方案是高效且适用于密钥管理服务系统的。

关键词: 密钥管理服务, SM4, 多方协同, Beaver乘法三元组

Abstract:

With the increasing demand for cryptograph localization and key protection, the composite application of commercial cryptographic algorithm and key security management has become one of the focuses of experts and scholars. In order to solve the problem of easy key disclosure in encryption/decryption scheme, this paper proposes a secure and efficient multi-party collaborative SM4 encryption/decryption scheme for key management service (KMS) system. The scheme uses the Beaver’s triple, which can be calculated predicatively and once, to construct a secure two-party multiplication and addition converter to ensure multi-party S-box collaborative computing, so as to realize the secure and efficient multi-party collaborative SM4 encryption/decryption and effectively reduce the computation and communication costs in the process of online interaction. Security analysis shows that the proposed scheme is secure under the malicious model and the other performance analysis details the computation and communication costs of the proposed scheme, which show that the proposed scheme is efficient and suitable for KMS system.

Key words: key management service, SM4, multi-party collaborate, Beaver’s triple

中图分类号:

TP309

杨伊, 何德彪, 文义红, 罗敏. 密钥管理服务系统下的多方协同SM4加/解密方案[J]. 信息网络安全, 2021, 21(8): 17-25.

YANG Yi, HE Debiao, WEN Yihong, LUO Min. Multi-party Collaborative SM4 Encryption/Decryption Scheme in Key Management Service[J]. Netinfo Security, 2021, 21(8): 17-25.

图/表 4

表1

符号及其定义

符号	定义
$\tau $	协同加/解密参与方个数
$i$	当前轮数,$i\in \{0,\cdots,31\}$
$j$	当前执行的S盒序号,$j\in \{0,\cdots,3\}$
${{P}_{\alpha }}$	协同加/解密参与方,$\alpha \in \{1,\cdots,\tau \}$
${{P}_{\beta }}$	协同加/解密参与方,$\beta \in \{1,\cdots,\tau \}$
$A$	域为2的8阶可逆矩阵,$A=\left( \begin{matrix} 1 & 1 & 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{matrix} \right)$
$f$	函数,输入为二进制数,输出为向量,即$f\text{(}a\text{)=}\mathbf{a}$
$C$	域为$GF({{2}^{8}})$的向量,$\mathbf{C}=(1,1,0,0,1,0,1,1)$
C_j	每轮单个S盒中使用的向量
$FK$,$CK$	128 bit系统参数,$FK=\ (F{{K}_{0}},F{{K}_{1}},F{{K}_{2}},F{{K}_{3}})$,$CK=\ (C{{K}_{0}},C{{K}_{1}},C{{K}_{2}},C{{K}_{3}})$
$\text{mod}\ M(x)$	模不可约多项式,$M\left( x \right)=\ {{x}^{8}}+{{x}^{7}}+{{x}^{6}}+{{x}^{5}}+{{x}^{4}}+{{x}^{3}}+{{x}^{2}}+1$
L	线性变换,$L(B)=B\oplus (B<<<2)\oplus (B<<<10)\oplus $ $(B<<<18)\oplus (B<<<24)$
L′	线性变换,$L´(B)=B\oplus (B<<<13)\oplus (B<<<23)$
$key$	128 bit加/解密密钥
$M$	128 bit消息
${{M}^{\alpha }}$	${{P}_{\alpha }}$拥有的部分消息
$ke{{y}^{\alpha }}$	${{P}_{\alpha }}$拥有的部分加/解密密钥
${{(a_{i}^{\alpha })}_{j}}$	${{P}_{\alpha }}$的S盒输入
${{(\mathbf{b}_{i}^{\alpha })}_{j}}$	${{P}_{\alpha }}$选择的随机向量,${{(\mathbf{b}_{i}^{\alpha })}_{j}}\in GF({{2}^{8}})$
$l_{i}^{\alpha }$	${{P}_{\alpha }}$的S盒输出
$r{{k}_{i}}$	32 bit轮密钥,$i\in \{0,\cdots,31\}$
$r{{k}_{i}}^{\alpha }$	${{P}_{\alpha }}$拥有的部分轮密钥
$EN$	128 bit密文
$E{{N}^{\alpha }}$	${{P}_{\alpha }}$产生的部分密文
$\pi _{mul}^{prive}$	一种基于安全两方计算的乘加转换器

表1

图1

表2

表3

参考文献 26

[1]	GM/T0002-2012 SM4 Block Cipher Algorithm[S]. Beijing: Standards Press of China, 2012.
	GM/T0002-2012 SM4分组密码算法[S]. 北京: 中国标准出版社, 2012.
[2]	REITER M K, FRANKLIN M K, LACY J B, et al. The Ω Key Management Service[J]. Journal of Computer Security, 1996, 4(4):267-287. doi: 10.3233/JCS-1996-4402 URL
[3]	CHALLAL Y, SEBA H. Group Key Management Protocols: A Novel Taxonomy[J]. International Journal of Information Technology, 2005, 2(1):105-118.
[4]	READY L B, ODEN R, CHADWICK H S, et al. Development of An Anesthesiology-based Postoperative Pain Management Service[J]. The Journal of the American Society of Anesthesiologists, 1988, 68(1):100-106.
[5]	TIAN Biming, HAN Song, LIU Liu, et al. Towards Enhanced Key Management in Multi-phase ZigBee Network Architecture[J]. Computer Communications, 2012, 35(5):579-588. doi: 10.1016/j.comcom.2011.12.004 URL
[6]	CHANDRAMOULI R, IORGA M, CHOKHANI S. Cryptographic Key Management Issues and Challenges in Cloud Services[J]. Secure Cloud Computing, 2014: 1-30.
[7]	TOMESCU A, CHEN R, ZHENG Yiming, et al. Towards Scalable Threshold Cryptosystems[C]//IEEE. 2020 IEEE Symposium on Security and Privacy, May 18-20, 2020, San Francisco, CA, USA. Piscataway: IEEE Press, 2020: 877-893.
[8]	HE Debiao, ZHANG Yudi, WANG Ding, et al. Secure and Efficient Two-party Signing Protocol for the Identity-based Signature Scheme in the IEEE P1363 Standard for Public Key Cryptography[J]. IEEE Transactions on Dependable and Secure Computing, 2018, 17(5):1124-1132. doi: 10.1109/TDSC.8858 URL
[9]	FENG Qi, HE Debiao, LIU Zhe, et al. Distributed Signing Protocol for IEEE P1363-compliant Identity-based Signature Scheme[J]. IET Information Security, 2020, 14(4):443-451. doi: 10.1049/ise2.v14.4 URL
[10]	ZHANG Yudi, HE Debiao, ZHANG Mingwu, et al. A Provable-secure and Practical Two-party Distributed Signing Protocol for SM2 Signature Algorithm[J]. Frontiers of Computer Science, 2020, 14(3):1-14. doi: 10.1007/s11704-019-8231-0 URL
[11]	MU Yongheng, XU Haixia, LI Peili, et al. Secure Two-party SM9 Signing[J]. SCIENCE CHINA Information Sciences, 2020, 63(8):1-3.
[12]	BOYLE E, GOLDWASSER S, TESSARO S. Communication Locality in Secure Multi-party Computation[C]// TCC. Theory of Cryptography Conference, March 3-6, 2003, Tokyo, Japan. Heidelberg: Springer, 2013: 356-376.
[13]	FENG Qi, HE Debiao, LUO Min, et al. Lightweight SM2 Two Party Cooperative Signature in Mobile Internet Environment[J]. Journal of Computer Research and Development, 2020, 57(10):2136-2146.
	冯琦, 何德彪, 罗敏, 等. 移动互联网环境下轻量级SM2两方协同签名[J]. 计算机研究与发展, 2020, 57(10):2136-2146.
[14]	SHAMIR A. How to Share a Secret[J]. Communications of the ACM, 1979, 22(11):612-613. doi: 10.1145/359168.359176 URL
[15]	HOU Hongxia, YANG Bo, ZHANG Lina, et al. Secure Two Party Cooperative SM2 Signature Algorithm[J]. Acta Electronica Sinica, 2019, 48(1):1-8.
	侯红霞, 杨波, 张丽娜, 等. 安全的两方协作SM2签名算法[J]. 电子学报, 2019, 48(1):1-8.
[16]	MACKENZIE P, REITER M K. Two-party Generation of DSA Signatures[C]// Springer. 21th Annual International Cryptology Conference, August 12-16, 2001, San Francisco, CA, USA. Berlin: Springer, 2001: 137-154.
[17]	LINDELL Y. Fast Secure Two-party ECDSA Signing[C]// Springer. 37th Annual International Cryptology Conference, August 20-24, 2017, Santa Barbara, CA, USA. Berlin: Springer, 2017: 613-644.
[18]	DOERNER J, KONDI Y, LEE E, et al. Secure Two-party Threshold ECDSA from ECDSA Assumptions[C]// IEEE. 2018 IEEE Symposium on Security and Privacy, May 20-24, 2018, San Francisco, CA, USA. Piscataway: IEEE Press, 2018: 980-997.
[19]	CHOU T, ORLANDI C. The Simplest Protocol for Oblivious Transfer[C]// Springer. 4th International Conference on Cryptology and Information Security in Latin America, August 23-26, 2015, Guadalajara, Mexico. Berlin: Springer, 2015: 40-58.
[20]	KELLER M, ORSINI E, SCHOLL P. Actively Secure OT Extension with Optimal Overhead[C]//Springer. 35th Annual Cryptology Conference, August 16-20, 2015, Santa Barbara, CA, USA. Berlin: Springer, 2015: 724-741.
[21]	BEAVER D. Efficient Multiparty Protocols Using Circuit Randomization[C]//Springer. 11th Annual International Cryptology Conference, August 11-15, 1991, Santa Barbara, CA, USA. Berlin: Springer, 1991: 420-432.
[22]	ZHANG Lei, WU Wenling. Differential Fault Attack of SM4 Cipher Algorithm[J]. Chinese Journal of Computers, 2006, 29(9):1596-1602.
	张蕾, 吴文玲. SM4密码算法的差分故障攻击[J]. 计算机学报, 2006, 29(9):1596-1602.
[23]	DONG Xiaoli. Security Analysis of AES and SM4 Block Ciphers[D]. Xi’an: Xidian University, 2011.
	董晓丽. 分组密码AES和SM4的安全性分析[D]. 西安:西安电子科技大学, 2011.
[24]	FENG Qi, HE Debiao, LIU Zhe, et al. Secure NLP: A System for Multi-party Privacy-preserving Natural Language Processing[J]. IEEE Transactions on Information Forensics and Security, 2020, 15(5):3709-3721. doi: 10.1109/TIFS.10206 URL
[25]	HUANG Kai, LIU Ximeng, FU Shaojing, et al. A Lightweight Privacy-preserving CNN Feature Extraction Framework for Mobile Sensing[J]. IEEE Transactions on Dependable and Secure Computing, 2019, 18(9):1441-1455.
[26]	CRAMER R, DAMGRD I, ESCUDERO D, et al. SPDZ2k: Efficient MPC for Dishonest Majority[C]// Springer. 38th Annual International Cryptology Conference, August 19-23, 2018, Santa Barbara, CA, USA. Berlin: Springer, 2018: 769-798.

参与方数量/个安全模型	2	15	45
半诚实模型	2.234	17.483	66.696
恶意模型	2.256	17.537	67.015

参与方数量/个安全模型	2	15	45
半诚实模型	32	3360	31680
恶意模型	64	3600	32400

密钥管理服务系统下的多方协同SM4加/解密方案

Multi-party Collaborative SM4 Encryption/Decryption Scheme in Key Management Service

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 4

参考文献 26

相关文章 3

编辑推荐

Metrics

本文评价

[1]	李秀滢, 吉晨昊, 段晓毅, 周长春. GPU上SM4算法并行实现[J]. 信息网络安全, 2020, 20(6): 36-43.
[2]	陈颖, 陈长松, 胡红钢. SM4硬件电路的功耗分析研究[J]. 信息网络安全, 2018, 18(5): 52-58.
[3]	王敏, 饶金涛, 吴震, 杜之波. SM4密码算法的频域能量分析攻击[J]. 信息网络安全, 2015, 15(8): 14-19.