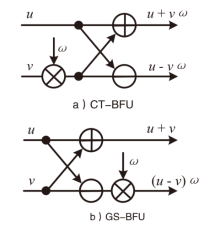
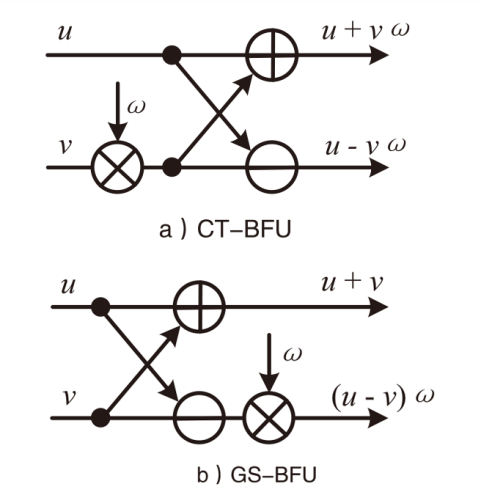
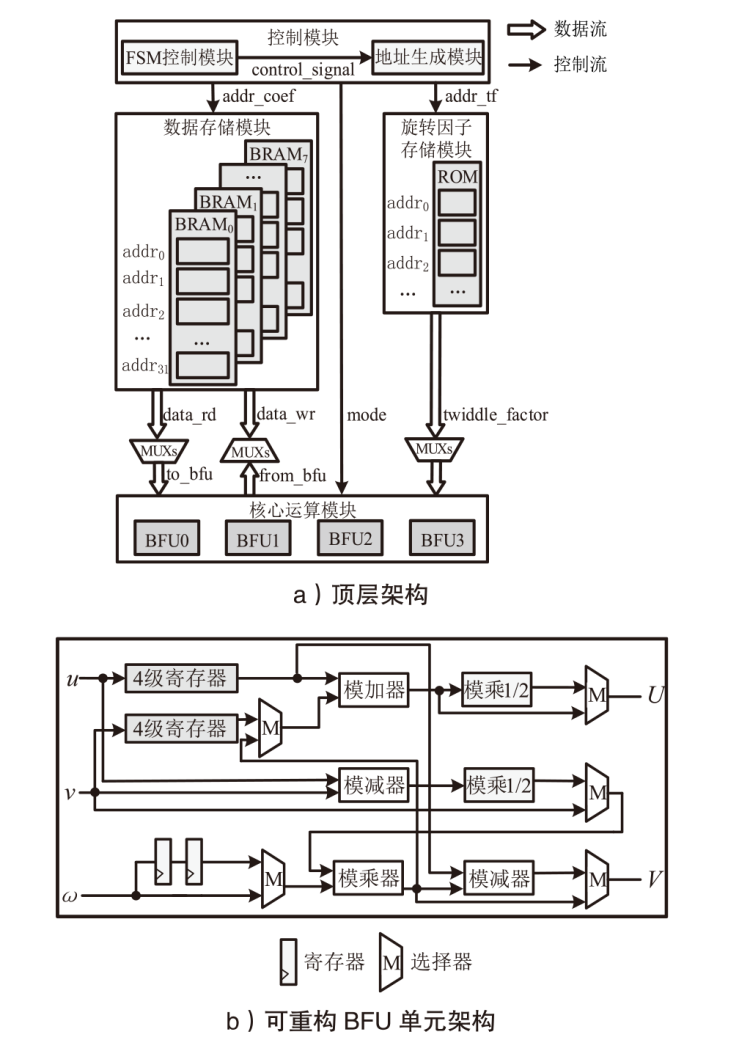
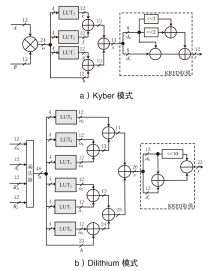
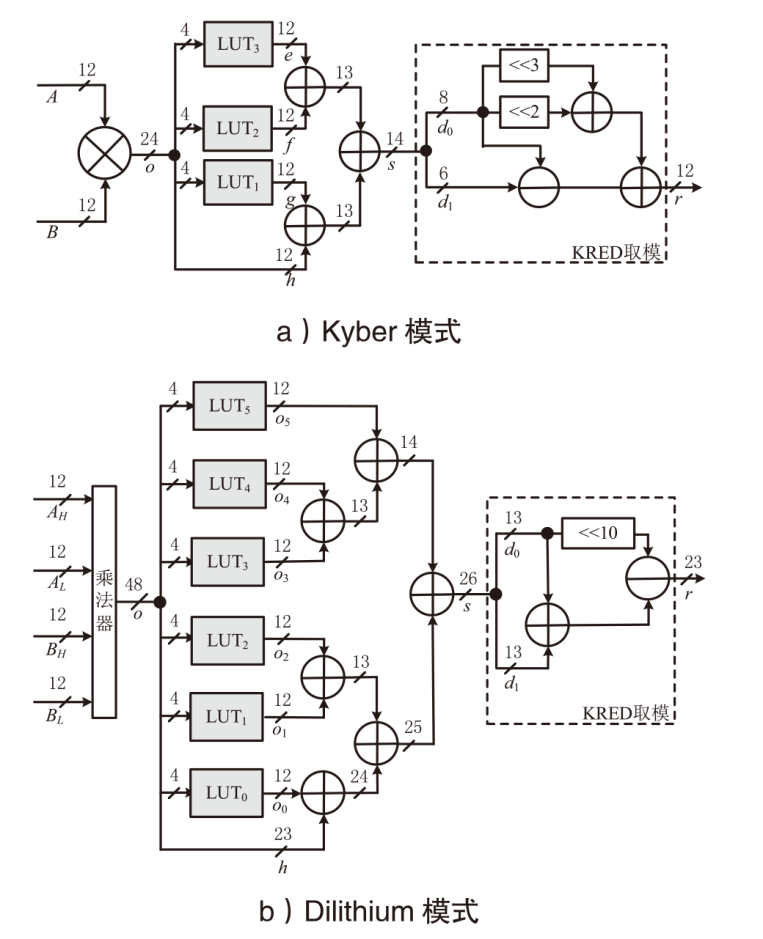
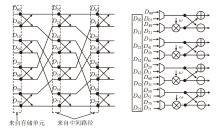
| [1] |
TAO Yunting, KONG Fanyu, YU Jia, et al. Survey of Number Theoretic Transform Algorithms for Quantum-Resistant Lattice-Based Cryptography[J]. Netinfo Security, 2021, 21(9): 46-51.
|
|
陶云亭, 孔凡玉, 于佳, 等. 抗量子格密码体制的快速数论变换算法研究综述[J]. 信息网络安全, 2021, 21(9):46-51.
|
| [2] |
ALAGIC G, ALPERIN-SHERIFF J, APON D, et al. Status Reporton the Second Round of the NIST Post-Quantum CryptographyStandardization Process[R]. Gaithersburg: NIST, 8309, 2020.
|
| [3] |
LIU Zhe, PÖPPELMANN T, ODER T, et al. High-Performance Ideal Lattice-Based Cryptography on 8-Bit AVR Microcontrollers[J]. ACM Transactions on Embedded Computing Systems (TECS), 2017, 16(4): 1-24.
|
| [4] |
ZHANG Neng, YANG Bohan, CHEN Chen, et al. Highly Efficient Architecture of New Hope-NIST on FPGA Using Low-Complexity NTT/INTT[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020(2): 49-72.
|
| [5] |
CHEN D D, MENTENS N, VERCAUTEREN F, et al. High-Speed Polynomial Multiplication Architecture for Ring-LWE and SHE Cryptosystems[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 62(1): 157-166.
|
| [6] |
REISIS D, VLASSOPOULOS N. Conflict-Free Parallel Memory Accessing Techniques for FFT Architectures[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(11): 3438-3447.
|
| [7] |
MERT A C, ÖZTÜRK E, SAVAŞ E. Design and Implementation of a Fast and Scalable NTT-Based Polynomial Multiplier Architecture[C]// IEEE. 2019 22nd Euromicro Conference on Digital System Design (DSD). New York: IEEE, 2019: 253-260.
|
| [8] |
CHEN Xiangren, YANG Bohan, YIN Shouyi, et al. CFNTT: Scalable Radix-2/4 NTT Multiplication Architecture with An Efficient Conflict-Free Memory Mapping Scheme[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2022(1): 94-126.
|
| [9] |
KIM D W, MAULANA D I, JUNG W. Kyber Accelerator on FPGA Using Energy-Efficient LUT-Based Barrett Reduction[C]// IEEE.19th International SoC Conference (ISOCC 2022). New York: IEEE, 2022: 83-84.
|
| [10] |
ZHAO Cankun, ZHANG Neng, WANG Hanning, et al. A Compact and High-Performance Hardware Architecture for Crystals-Dilithium[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2022(1): 270-295.
|
| [11] |
NGUYEN D T, DANG V B, GAJ K. High-Level Synthesis in Implementing and Benchmarking Number Theoretic Transform in Lattice-Based Post-Quantum Cryptography Using Software/Hardware Codesign[C]// Springer. Applied Reconfigurable Computing. Architectures, Tools, and Applications:16th International Symposium (ARC 2020). Heidelberg: Springer, 2020: 247-257.
|
| [12] |
LONGA P, NAEHRIG M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography[C]// Springer.Cryptology and Network Security:15th International Conference (CANS 2016). Heidelberg: Springer, 2016: 124-139.
|
| [13] |
YE Zewen, CHEUNG R C C, HUANG Kejie. PipeNTT: A Pipelined Number Theoretic Transform Architecture[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(10): 4068-4072.
|
| [14] |
DERYA K, MERT A C, ÖZTÜRK E, et al. CoHA-NTT: A Configurable Hardware Accelerator for NTT-Based Polynomial Multiplication[EB/OL]. [2024-02-20]. https://www.xueshufan.com/publication/3216016201.
|
| [15] |
BISHEH-NIASAR M, AZARDERAKHSH R, MOZAFFARI-KERMANI M. Instruction-Set Accelerated Implementation of CRYSTALS-Kyber[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(11): 4648-4659.
|
| [16] |
YAMAN F, MERT A C, ÖZTÜRK E, et al. A Hardware Accelerator for Polynomial Multiplication Operation of CRYSTALS-KYBER PQC Scheme[C]// IEEE. 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE). New York: IEEE, 2021: 1020-1025.
|
| [17] |
MAO Gaoyu, CHEN Donglong, LI Guangyan, et al. High-Performance and Configurable SW/HW Co-Design of Post-Quantum Signature CRYSTALS-Dilithium[J]. ACM Transactions on Reconfigurable Technology and Systems, 2023, 16(3): 1-28.
|
| [18] |
ZHOU Zhen, HE Debiao, LIU Zhe, et al. A Software/Hardware Co-Design of Crystals-Dilithium Signature Scheme[J]. ACM Transactions on Reconfigurable Technology and Systems (TRETS), 2021, 14(2): 1-21.
|