Quantum Solving Euler’s Totient Function to Crack RSA

doi:10.3969/j.issn.1671-1122.2023.07.001

Abstract

Abstract:

Quantum computing is a novel computing mode based on the principles of quantum mechanics, which has the natural advantages of parallel computing. Shor’s algorithm is an algorithm that can quickly decompose integers and is expected to crack RSA encryption technology. However, Shor’s algorithm is difficult to be implemented on a quantum computer due to the fact that the modular power circuit to be constructed is extremely complex, and the number of qubits affects the accuracy of the subsequent continued fractions. To solve the above problems, this paper proposed a new algorithm based on the knowledge of number theory and RSA algorithm, designed relevant quantum circuits to solve the Euler’s totient function of the integer N to be decomposed. After the Euler’s totient function of the integer N to be decomposed was solved by quantum computing, the two prime factors could be obtained by constructing and solving a system of binary linear equations. Moreover, the private key could be further calculated by combining the public key, so as to crack the ciphertext. On the basis of universality, this algorithm only uses 2n+2 qubits, only needs to solve the modular multiplication of numbers, and does not need to calculate continued fractions.

Key words: quantum computing, Shor’s algorithm, RSA algorithm, Euler’s totient function

CLC Number:

TP309

ZHANG Xinglan, ZHANG Feng. Quantum Solving Euler’s Totient Function to Crack RSA[J]. Netinfo Security, 2023, 23(7): 1-8.

Figures/Tables 10

References 27

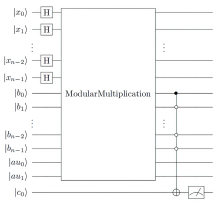
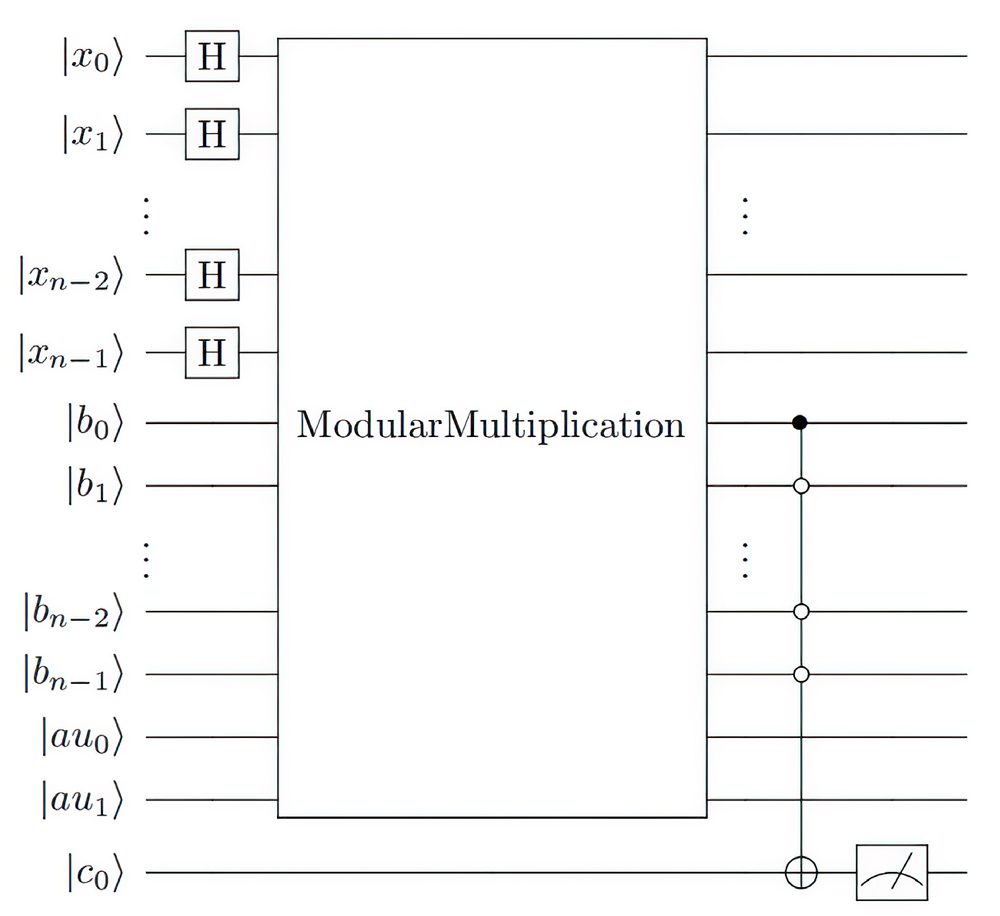
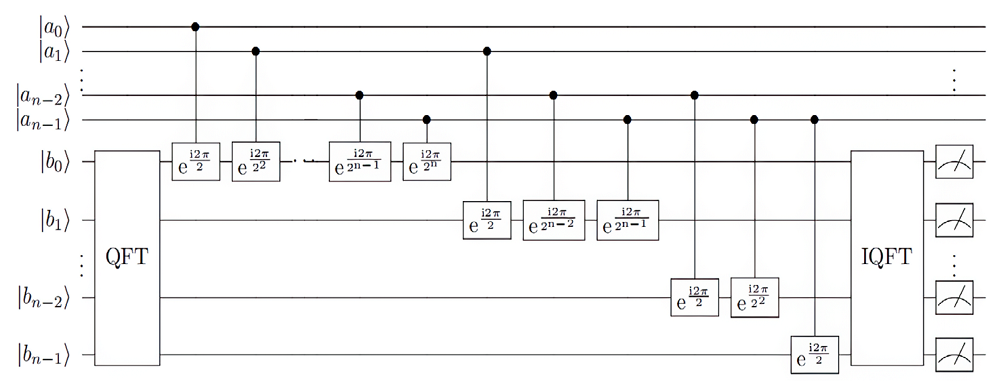
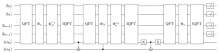
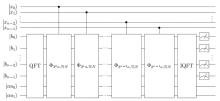
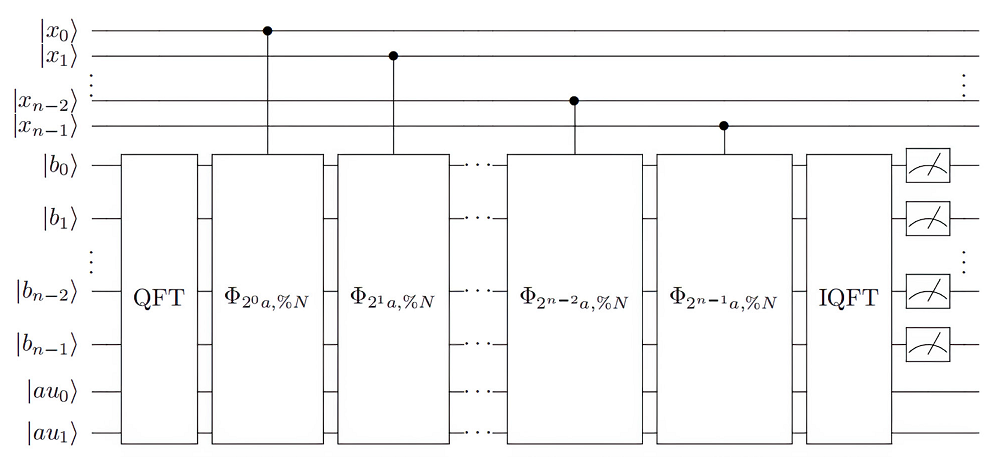
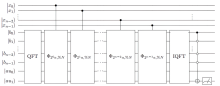
[1]	FEYNMAN R P. Simulating Physics with Computers[J]. International Journal of Theoretical Physics, 1982, 21(6): 467-488. doi: 10.1007/BF02650179 URL
[2]	ARUTE F, ARYA K, BABBUSH R, et al. Quantum Supremacy Using a Programmable Superconducting Processor[J]. Nature, 2019, 574(7779): 505-510. doi: 10.1038/s41586-019-1666-5
[3]	BHATIA V, RAMKUMAR K R. An Efficient Quantum Computing Technique for Cracking RSA Using Shor's Algorithm[C]// IEEE. 5th International Conference on Computing Communication and Automation. New York: IEEE, 2020: 89-94.
[4]	MASLOV D, NAM Y, KIM J. An Outlook for Quantum Computing[J]. Proceedings of the IEEE, 2018, 107(1): 5-10. doi: 10.1109/JPROC.2018.2884353 URL
[5]	NIELSEN M A, CHUANG I L. Quantum Computation and Quantum Information[M]. Cambridge: Cambridge University Press, 2010.
[6]	DEUTSCH D, JOZSA R. Rapid Solution of Problems by Quantum Computation[J]. Proceedings of the Royal Society A, 1992, 439(1907): 553-558.
[7]	SHOR P W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring[C]// IEEE. Proceedings 35th Annual Symposium on Foundations of Computer Science. Piscataway: IEEE, 1994: 124-134.
[8]	GROVER L K. A Fast Quantum Mechanical Algorithm for Database Search[C]// ACM. Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing. New York: ACM. 1996: 212-219.
[9]	HARROW A W, HASSIDIM A, LLOYD S. Quantum Algorithm for Linear Systems of Equations[EB/OL].(2009-07-5) [2022-12-10]. https://doi.org/10.1103/PhysRevLett.103.150502.
[10]	LI Zhaokai, LIU Xiaomei, XU Nanyang, et al. Experimental Realization of a Quantum Support Vector Machine[EB/OL]. (2014-12-01) [2022-12-10]. https://doi.org/10.1103/PhysRevLett.114.140504.
[11]	LLOYD S, MOHSENI M, REBENTROST P. Quantum Principal Component Analysis[J]. Nature Physics, 2014, 10(9): 631-633. doi: 10.1038/nphys3029
[12]	OHZEKI M. Message-Passing Algorithm of Quantum Annealing with Nonstoquastic Hamiltonian[EB/OL]. (2019-04-17) [2022-12-10]. https://doi.org/10.7566/JPSJ.88.061005.
[13]	ZHANG Guofeng, HAMDULLA A. Adaptive Morphological Contrast Enhancement Based on Quantum Genetic Algorithm for Point Target Detection[J]. Mobile Networks and Applications, 2021, 26(2): 638-648. doi: 10.1007/s11036-019-01410-8
[14]	AMICO M, SALEEM Z H, KUMPH M. Experimental Study of Shor's Factoring Algorithm Using the IBM Q Experience[EB/OL]. (2019-03-02) [2022-12-10]. https://doi.org/10.1103/PhysRevA.100.012305.
[15]	RIVEST R L, SHAMIR A, ADLEMAN L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120-126. doi: 10.1145/359340.359342 URL
[16]	GAMEL O, JAMES D F V. Simplified Factoring Algorithms for Validating Small-Scale Quantum Information Processing Technologies[EB/OL]. (2013-11-14) [2022-12-10]. https://doi.org/10.48550/arXiv.1310.6446.
[17]	GELLER M R, ZHOU Z. Factoring 51 and 85 with 8 Qubits[J]. Scientific reports, 2013, 3(1): 1-5.
[18]	MOUSAVI M, HOUSHMAND M, BOLOKIAN M. The Cost Reduction of Distributed Quantum Factorization Circuits[J]. International Journal of Theoretical Physics, 2021, 60(4): 1292-1298. doi: 10.1007/s10773-021-04756-6
[19]	SKOSANA U, TAME M. Demonstration of Shor’s Factoring Algorithm for N \$\$= \$\$= 21 on IBM Quantum Processors[J]. Scientific Reports, 2021, 11(1): 1-12. doi: 10.1038/s41598-020-79139-8
[20]	CHERVENAK A, VELLANKI V, KURMAS Z. Protecting File Systems: A Survey of Backup Techniques[C]// ACM. Joint NASA and IEEE Mass Storage Conference. New York: ACM. 1998: 17-31.
[21]	WIENER M J. Cryptanalysis of Short RSA Secret Exponents[J]. IEEE Transactions on Information theory, 1990, 36(3): 553-558. doi: 10.1109/18.54902 URL
[22]	BONEH D. Twenty Years of Attacks on the RSA Cryptosystem[J]. Notices of the AMS, 1999, 46(2): 203-213.
[23]	SHAND M, VUILLEMIN J. Fast Implementations of RSA Cryptography[C]// IEEE. Proceedings of IEEE 11th Symposium on Computer Arithmetic. New York: IEEE, 1993: 252-259.
[24]	BEAUREGARD S. Circuit for Shor's Algorithm Using 2n+3 Qubits[J]. Quantum Information & Computation, 2003, 3(2): 175-185.
[25]	DRAPER T G. Addition on a Quantum Computer[EB/OL]. (2000-08-07) [2022-12-10]. https://doi.org/10.48550/arXiv.quant-ph/0008033.
[26]	CROSS A. The IBM Q Experience and Qiskit Open-Source Quantum Computing Software[C]// APS. APS March Meeting Abstracts. Maryland: APS, 2018: 53-58.
[27]	DA S A J, PARK D K. Linear-Depth Quantum Circuits for Multiqubit Controlled Gates[EB/OL]. (2022-09-07) [2022-12-10]. https://doi.org/10.1103/PhysRevA.106.042602.

Qiskit Software	Version
qiskit-terra	0.21.2
qiskit-aer	0.10.4
qiskit-ignis	0.7.1
qiskit-ibmq-provider	0.19.2
qiskit	0.37.2
Python version	3.8.0
Python compiler	Clang 4.0.1 (tags/RELEASE_401/final)
Python build	default, Nov 6 2019 15:49:01
OS	macOS Monterey 12.5.1
CPU	8
Memory (GB)	16