基于混沌和改进广义Feistel结构的轻量级密码算法

doi:10.3969/j.issn.1671-1122.2022.08.002

摘要/Abstract

摘要：

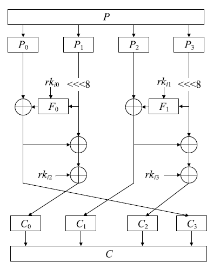
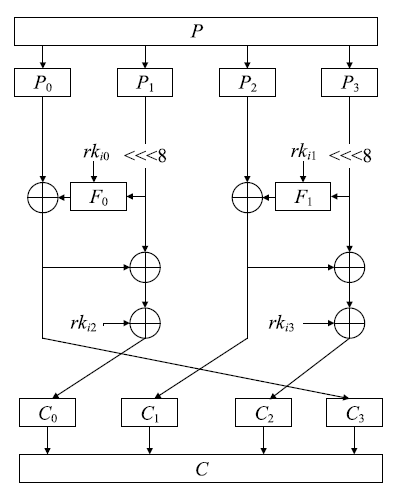
随着物联网的快速发展,无线网络传感器、射频识别标签以及工业控制器等被广泛部署,这些资源受限设备的安全同样需要保障,而传统的密码算法需要消耗大量的资源,不适用于资源受限设备。针对以上问题,文章提出一种轻量级分组密码。S盒是分组密码的关键性组件,通过应用两个混沌映射和跳跃蜘蛛优化算法构成的多目标优化算法生成并优化得到非线性度平均值为110,线性逼近概率为0.1172,差分逼近概率为0.0391的S盒。文章对广义Feistel结构进行相应改进,改进后的结构一次能够处理所有的中间状态,不存在未处理的分支,并结合构造的S盒、密钥扩展算法等,组成分组长度为64位、种子密钥长度为80位、迭代轮数为12轮的轻量级分组密码算法。该算法的等效门电路数量符合轻量级的标准,并且有良好的性能。

关键词: 轻量级分组密码, S盒, 广义Feistel结构, 混沌映射, 跳跃蜘蛛优化算法

Abstract:

With the rapid development of the Internet of Things, wireless network sensors, radio frequency identification tags, and industrial controllers are widely deployed. The security of these limited devices also needs to be guaranteed, and the traditional cryptographic algorithm needs to consume a lot of resources. To solve these problems, a new lightweight block cipher was proposed. S-box was a key component in block cipher. By applying two chaotic map, a S-box with average nonlinearity of 110, linear approximation probability of 0.1172 and differential approximation probability of 0.0391 was obtained. The generalized Feistel structure was correspondingly improved and the improved structure could handle all intermediate states at one time without unprocessed branches. Combined with the constructed S-box, the improved structure and key expansion algorithm, a new lightweight block cipher algorithm with a packet length of 64 bit, a seed key length of 80 bit and 12 iteration rounds was formed. The algorithm has good performance and the gate equivalent number of that meets the lightweight standard.

Key words: lightweight block cipher, S-box, generalized Feistel structure, chaotic map, jumping spiders optimization algorithm

中图分类号:

TP309

佟晓筠, 苏煜粤, 张淼, 王翥. 基于混沌和改进广义Feistel结构的轻量级密码算法[J]. 信息网络安全, 2022, 22(8): 8-18.

TONG Xiaojun, SU Yuyue, ZHANG Miao, WANG Zhu. Lightweight Cipher Algorithm Based on Chaos and Improved Generalized Feistel Structure[J]. Netinfo Security, 2022, 22(8): 8-18.

图/表 16

图1

图2

图3

表1

表2

表3

表4

表5

表6

图4

表7

表8

图5

表9

表10

图6

参考文献 31

[1]	SMID M E, BRANSTAD D K. The Data Encryption Standard: Past and Future[J]. Proceedings of the IEEE, 1988, 76(5): 550-559. doi: 10.1109/5.4441 URL
[2]	DAEMEN J, RIJMEN V. The Design of Rijndael: AES—The Advanced Encryption Standard[M]. Berlin: Springer, 2002.
[3]	SCHNEIER B. The IDEA Encryption Algorithm[J]. Dr Dobb’s Journal-Software Tools for the Professional Programmer, 1993, 18(13): 50-57.
[4]	LI Lang, LIU Botao, WANG Hui. QTL: A New Ultra-Lightweight Block Cipher-Science Direct[J]. Microprocessors and Microsystems, 2016, 45(1): 45-55. doi: 10.1016/j.micpro.2016.03.011 URL
[5]	LI Lang, LI Kenli, HE Weiwei, et al. Magpie: A High Security Lightweight Block Cipher Algorithm[J]. Acta Electronica Sinica, 2017, 45(10): 2521-2527. doi: 10.3969/j.issn.0372-2112.2017.10.029
	李浪, 李肯立, 贺位位, 等. Magpie:一种高安全的轻量级分组密码算法[J]. 电子学报, 2017, 45(10):2521-2527. doi: 10.3969/j.issn.0372-2112.2017.10.029
[6]	BISWAS A, MAJUMDAR A, NATH S, et al. LRBC: A Lightweight Block Cipher Design for Resource Constrained IoT Devices[EB/OL]. (2020-01-11)[2022-04-11]. https://doi.org/10.1007/s12652-020-01694-9.
[7]	LI Lang, LIU Botao. Surge: A New Low-Resource and Efficient Lightweight Block Cipher Algorithm[J]. Computer Science, 2018, 45(2): 236-240.
	李浪, 刘波涛. Surge:一种新型、低资源、高效的轻量级分组密码算法[J]. 计算机科学, 2018, 45(2):236-240.
[8]	LI Lang, LIU Botao, ZHOU Yimeng, et al. SFN: A New Lightweight Block Cipher[J]. Microprocessors and Microsystems, 2018, 60: 138-150. doi: 10.1016/j.micpro.2018.04.009 URL
[9]	FENG Jingya, LI Lang. SCENERY: A Lightweight Block Cipher Based on Feistel Structure[J]. Frontiers of Computer Science, 2022, 16(3): 1-10.
[10]	SHI Guodong, KANG Fei, GU Haiwen. Research on Unified Description Model of Block Cipher[J]. Computer Engineering, 2010, 36(1): 154-156.
	师国栋, 康绯, 顾海文. 分组密码统一描述模型研究[J]. 计算机工程, 2010, 36(1): 154-156.
[11]	DWIVEDI A D. BRISK: Dynamic Encryption Based Cipher for Long Term Security[EB/OL]. (2021-08-26)[2022-04-13]. https://doi.org/10.3390/s21175744.
[12]	TONG Xiaojun, LIU Xudong, LIU Jing, et al. A Novel Lightweight Block Encryption Algorithm Based on Combined Chaotic S-Box[EB/OL]. (2021-09-18)[2022-04-13]. https://doi.org/10.1142/S0218127421501522.
[13]	ZHANG Xiaofeng, LIU Yonggui. Lightweight Block Cipher Algorithm Based on the Improved Generalized Feistel Structure[EB/OL]. (2021-08-26)[2022-04-13]. .
	张晓枫, 刘永桂. 改进的广义Feistel结构轻量级分组密码算法[EB/OL]. (2021-08-26)[2022-04-13]. http://kns.cnki.net/kcms/detail/44.1240. TP.20210825.1338.020. html.
[14]	MASSEY J L. SAFER K-64: A Byte-Oriented Block-Ciphering Algorithm[C]//Springer. International Workshop on Fast Software Encryption. Berlin: Springer, 1993: 1-17.
[15]	LAMBIC D. A Novel Method of S-Box Design Based on Discrete Chaotic Map[J]. Nonlinear Dynamics, 2017, 87(4): 1-7. doi: 10.1007/s11071-016-2940-9 URL
[16]	HEMATPOUR N, AHADPOUR S. Execution Examination of Chaotic S-Box Dependent on Improved PSO Algorithm[J]. Neural Computing and Applications, 2021, 33(10): 5111-5133. doi: 10.1007/s00521-020-05304-9 URL
[17]	WANG Yong, ZHANG Zhiqiang, ZHANG L Y, et al. A Genetic Algorithm for Constructing Bijective Substitution Boxes with High Nonlinearity[J]. Information Sciences, 2020, 523: 152-166. doi: 10.1016/j.ins.2020.03.025 URL
[18]	IBRAHIM S, ABBAS A M. A Novel Optimization Method for Constructing Cryptographically Strong Dynamic S-Boxes[J]. IEEE Access, 2020, 8: 225004-225017. doi: 10.1109/ACCESS.2020.3045260 URL
[19]	ZHANG Xuefeng, WEI Kaili, JIANG Wen. The Nonlinearity Optimization Algorithm of S-Box Based on TD-ERCS Sequence[J]. Netinfo Security, 2021, 21(1): 10-18.
	张雪锋, 卫凯莉, 姜文. 基于TD-ERCS序列的S盒非线性度优化算法[J]. 信息网络安全, 2021, 21(1): 10-18.
[20]	WANG Xingyuan, CHEN Xuan. An Image Encryption Algorithm Based on Dynamic Row Scrambling and Zigzag Transformation[EB/OL]. (2021-06-27)[2022-04-13]. https://doi.org/10.1016/j.chaos.2021.110962.
[21]	PERAZA V H, PENA D A, RANJAN P, et al. A Bio-Inspired Method for Mathematical Optimization Inspired by Arachnida Salticidade[EB/OL]. (2021-12-29)[2022-04-14]. https://doi.org/10.3390/math10010102.
[22]	WANG Xingyuan, GUAN Nana, YANG Jingjing. Image Encryption Algorithm with Random Scrambling Based on One-Dimensional Logistic Self-Embedding Chaotic Map[J]. Chaos Solitons and Fractals, 2021, 150(3): 111-117.
[23]	NARUEI I, KEYNIA F. A New Optimization Method Based on Coot Bird Natural Life Model[EB/OL]. (2021-11-15)[2022-04-13]. https://doi.org/10.1016/j.eswa.2021.115352.
[24]	TALATAHARI S, AZIZI M. Chaos Game Optimization: A Novel Metaheuristic Algorithm[J]. Artificial Intelligence Review, 2021, 54(2): 917-1004. doi: 10.1007/s10462-020-09867-w URL
[25]	VILLUENDAS R Y, VELAZQUEZ R J L, ALANIS T M D, et al. Mexican Axolotl Optimization: A Novel Bioinspired Heuristic[EB/OL]. (2021-04-03)[2022-04-13].https://doi.org/10.3390/math9070781.
[26]	CHOU J S, TROUNG D N. A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean[EB/OL]. (2021-01-15)[2022-04-13]. https://doi.org/10.1016/j.amc.2020.125535.
[27]	BELAZI A, KHAN M, ABD E L A A, et al. Efficient Cryptosystem Approaches: S-Boxes and Permutation-Substitution-Based Encryption[J]. Nonlinear Dynamics, 2017, 87(1): 337-361. doi: 10.1007/s11071-016-3046-0 URL
[28]	ULLAH A, JAMAL S S, SHAH T. A Novel Construction of Substitution Box Using a Combination of Chaotic Maps with Improved Chaotic Range[J]. Nonlinear Dynamics, 2017, 88(4): 2757-2769. doi: 10.1007/s11071-017-3409-1 URL
[29]	HUA Zhongyun, LI Jiaxin, CHEN Yongyong, et al. Design and Application of an S-Box Using Complete Latin Square[J]. Nonlinear Dynamics, 2021, 104(1): 807-825. doi: 10.1007/s11071-021-06308-3 URL
[30]	BOGDANOV A, KNUDSEN L R, LEANDER G, et al. PRESENT: An Ultra-Lightweight Block Cipher[C]//Springer. Cryptographic Hardware and Embedded Systems-CHES 2007, 9th International Workshop. Berlin: Springer, 2007: 450-466.
[31]	SHIRAI T, SHIBUTANI K, AKISHITA T, et al. The 128-bit Blockcipher CLEFIA (Extended Abstract)[M]. Berlin: Lecture Notes in Computer Science, 2007.

S-Box	MIN-NL	MAX-NL	AVG-NL	LP	DP	SAC	BIC- NL	BIC-SAC
文献[27]方案	102	108	105.3	0.1563	0.0391	0.5056	103.79	0.5023
文献[28]方案	106	108	106.8	0.1250	0.0625	0.4939	106.57	0.4987
文献[29]方案	102	108	105.3	0.1406	0.0547	0.5352	103.21	0.4966
本文方案	110	110	110.0	0.1172	0.0391	0.5027	103.79	0.5012

列行	1	2	3	4	5	6	7	8
1	0.4688	0.4688	0.4844	0.4844	0.5313	0.5625	0.4844	0.5156
2	0.5781	0.5156	0.4844	0.4531	0.4844	0.4531	0.5000	0.4688
3	0.5156	0.4844	0.5000	0.5000	0.5000	0.5156	0.4688	0.5156
4	0.4844	0.4531	0.4844	0.5156	0.6094	0.5313	0.5313	0.4844
5	0.5000	0.5469	0.4688	0.4688	0.5469	0.4688	0.5000	0.5313
6	0.5156	0.5000	0.5000	0.4531	0.4688	0.5469	0.5156	0.4688
7	0.5469	0.4688	0.4688	0.5313	0.5781	0.5313	0.4844	0.5313
8	0.4531	0.5469	0.5313	0.4375	0.5000	0.5781	0.5156	0.4375

列行	1	2	3	4	5	6	7	8
1	0.5000	0.4961	0.4961	0.5098	0.4824	0.5000	0.5234	0.4805
2	0.4961	0.5000	0.4902	0.5020	0.4863	0.4863	0.5039	0.5098
3	0.4961	0.4902	0.5000	0.5078	0.5020	0.5078	0.5117	0.4922
4	0.5098	0.5020	0.5078	0.5000	0.5078	0.5020	0.4883	0.5137
5	0.4824	0.4863	0.5020	0.5078	0.5000	0.5137	0.4961	0.4941
6	0.5000	0.4863	0.5078	0.5020	0.5137	0.5000	0.5000	0.5078
7	0.5234	0.5039	0.5117	0.4883	0.4961	0.5000	0.5000	0.5254
8	0.4805	0.5098	0.4922	0.5137	0.4941	0.5078	0.5254	0.5000

模块	GE数
明文存储（64比特）	384
密钥存储（80比特）	480
S盒（轮函数）	400
S盒（密钥流）	100
P盒	0
异或（密钥流）	10.8
异或（轮函数）	86.4
异或（结构）	259.2
异或（CBC模式）	172.8
总计	1893.2

密码算法	密文长度/B
密码算法	10000	50000	100000
CLEFIA^[31]	0.00280	0.00006	0.00031
DES^[1]	0.00550	0.00480	0.00480
AES^[2]	0.00170	0.00130	0.00150
本文	0.00220	0.00003	0.00078