0 引言
金融信息化和金融安全是国家信息化的重要组成部分,国家信息化建设需要网络安全,而密码技术则是网络安全保障体系的重要支撑。为推动商用密码在金融和重要领域的全面应用,并做到自主可控,自2010年起,国家密码管理局制定并陆续发布了SM系列算法,包括SM1(SCB2)、SM2、SM3、SM4、SM9等。
随着商用密码算法的发布,与国产密码应用场景相关的标准体系也逐步建立,形成了较完整的产业链条。而在此之前,我国金融行业长期沿用3DES、AES、SHA、RSA等国际通用的密码算法体系和标准,信息技术安全可控程度低。此外,国密算法应用普及面临着实现效率低、缺乏丰富的软件形态密码产品等问题,使得国密算法替换国外密码算法后难以满足业务高效运转的需求,也无法满足云端、移动端、IoT等新场景的要求。为推进国密算法在金融业的应用工作,各金融机构均已着手重要系统的国产密码改造与应用试点,并在试点中不断探索实际遇到的问题和困难。
目前,业内对国密算法在实际应用中的软件性能与对标的国际密码算法的差异性研究较少,而此类研究可为国密软件开发厂商优化其SDK性能提供有效的机制保障,有助于国密算法改造工作的有效开展。
本文对SM3、SM2、SM4国密算法及对标的国际密码算法的设计原理进行比较,分析算法异同点,并进行算法间的计算量及安全性对比。首先,为验证理论分析所得的结论,对各算法基于C语言的代码实现进行性能测试验证。然后,在实际应用条件下,对经过优化的算法实现进行性能测试,将测试结果与理论分析结果的差异做深入研究。最后给出研究分析结果,并提出国密算法的优化建议。
为直观测算对比算法间的性能差异,本文的测试遵循如下原则。
1)SM2、SM3、SM4算法采用OpenSSL实现版本与我国A厂商优化版本进行对比测试,所有参与对比测试的国际算法均采用OpenSSL 1.1.1b版本实现。
2)采用单线程测试方法,排除多线程测试时由线程间切换调度等因素造成的对算法性能分析的干扰。
3)每轮输入随机产生的大小写字母与数字混合的字符串,每个输入长度运算10轮,去除一个最大值和一个最小值后取平均值作为测试结果,排除单次测试的偶然性。
4)每轮循环次数为N次(N根据算法耗时不同设定不同的数值),并且第一次运算结果不计算在内,避免了初始化和字符串加载缓存对结果的影响。此外,对所有算法的测试环境均相同。
1 杂凑算法
1.1 SM3与SHA-256
SM3与SHA系列算法的整体步骤相同,SM3算法包括消息填充、迭代压缩、得到杂凑值3个步骤。相较于SHA-256,SM3算法的压缩函数中增加了消息双字介入、P置换等设计,压缩函数更复杂,可抵抗强碰撞性的差分分析、弱碰撞性的线性分析等密码分析攻击[4]。鉴于压缩函数设计的复杂性,可以认为SM3的安全性比SHA-256的安全性略高。
1.2 算法计算量
SM3与SHA-256的算法结构相似、步骤相同,主要区别在于核心的迭代压缩步骤,该步骤包含消息扩展和状态更新两个子步骤。
两种算法均采用移位运算、逻辑运算、模232算数加的混合运算方法,但运算量不同。对两种算法的总体运算量做具体统计分析,将比特移位运算记为SH,将字(32 bit)与、或、异或、非等逻辑运算统一记为LO,将字模232算数加运算记为MA,得到SM3与SHA-256的迭代压缩步骤计算量对比如表1所示。
表1 SM3与SHA-256的迭代压缩步骤计算量对比
| 杂凑算法 | 消息扩展 | 状态更新 | 合计 |
|---|---|---|---|
| SM3 | 416SH+584LO | 1024SH+1328LO+ 384MA | 1440SH+1912LO+ 384MA |
| SHA-256 | 480SH+384LO+ 144MA | 768SH+1152LO+ 256MA | 1248SH+1536LO+ 400MA |
由表1可知,SHA-256算法的模数运算相对较多,而SM3算法的移位、逻辑运算等简单运算较多,其中模数运算比移位或逻辑运算等简单运算更耗时。总体而言,SM3的总体计算量与SHA-256相近。
1.3 算法性能测试分析
1.3.1 算法性能对比
对A厂商SM3、OpenSSL SM3和SHA-256算法的C语言实现进行性能测试,循环次数N=5000,分别测试在12组不同输入长度情况下两种算法的运行时间比(以SHA-256为基准),其中部分数据如表2所示。
表2 在不同输入长度下A厂商SM3、OpenSSL SM3与SHA-256的运行时间比
| 输入长度 | 运行时间比 | |
|---|---|---|
| A厂商SM3/SHA-256 | OpenSSL SM3/SHA-256 | |
| 8 B | 1.3819 | 1.8048 |
| 64 B | 1.2329 | 1.8392 |
| 256 B | 1.1652 | 1.9581 |
| 1 KB | 1.1295 | 2.0152 |
| 512 KB | 1.1181 | 2.0292 |
| 1 MB | 1.1160 | 2.0546 |
根据表2可知,A厂商SM3和OpenSSL SM3算法的耗时均略多于SHA-256算法,但两种SM3算法的软件性能相近,这与算法计算量分析结论相符。
1.3.2 优化对算法性能的影响
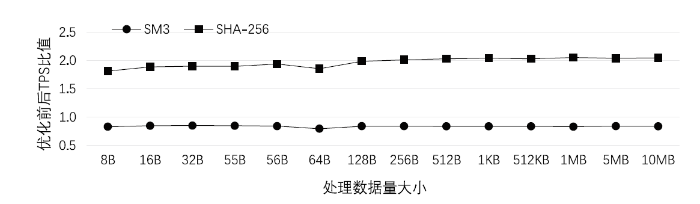
图1
由图1可以看出,SHA-256算法取得了良好的优化效果,优化后的性能约为优化前的两倍,SM3算法的性能则有所下降。
经分析发现,SHA-256算法在gcc编译器的O3级优化、宏定义等多种优化方法的作用下,取得了较好的优化效果,算法性能得到明显提升。以宏定义优化方法为例,将SHA-256算法的_asm块定义为C宏,在C代码中嵌入利用SIMD(Single Instruction Multiple Data,单指令多数据流)技术的汇编代码,进而实现算法优化。
结合1.3.1节的测试分析结果可知,SM3算法的性能应与SHA-256算法相近。由1.3.2节的测试情况可知,优化后的SHA-256算法使其软件性能得到较大提升,但SM3算法的性能下降。由此可见,通过算法优化,SHA-256杂凑算法的性能明显高于SM3算法,SM3算法没有通过编译进行优化的能力,需要进一步进行分析。
2 公钥算法
公钥算法基于非对称密码体制进行加密,加密密钥(公钥)与解密密钥(私钥)不同,且由已知加密密钥推导出解密密钥在计算上是不可行的。公钥算法可用于保证消息的机密性与完整性,分为数字签名和公钥加密两种应用场景,主要应用于对信息发送者的身份认证、信息加密等。
在全球范围内的各类系统中,应用范围最广的公钥算法是RSA。此外,由于基于ECC的算法具有加密速度快、密钥长度短等优势,逐渐得到业内的认可。国密公钥算法为SM2[5],本文将SM2算法与国际ECC算法、RSA算法进行对比,对国密算法的推广具有重要的参考价值。
就算法能够提供的安全等级而言,SM2算法的安全级别与基于256 bit域的国际ECC算法相当。
2.1 数字签名
在数字签名中,一般先将消息进行杂凑运算,生成较短的、固定长度的杂凑值,然后使用一种签名算法对杂凑值进行签名。因此,必须在数字签名中排除杂凑算法的干扰。本文将对SM2算法、ECDSA算法、RSA算法应用于数字签名的算法性能进行比较。
2.1.1 SM2、ECDSA与RSA
SM2数字签名算法与ECDSA算法均基于ECC上的离散对数困难问题,均由系统参数和辅助函数选取、签名算法、签名验证算法3个步骤组成。两种算法的整体结构相似[8],主要区别如下。
1)椭圆曲线的选取不同;
2)杂凑函数选取不同;
3)处理待签名消息的方式不同;
4)签名计算方式不同。
2.1.2 数字签名算法计算量
SM2数字签名算法与ECDSA算法的整体结构相似,主要区别是杂凑函数的选取与签名的计算方式不同。考虑数字签名算法直接对杂凑值进行签名与签名验证,因此在对SM2数字签名算法与ECDSA算法进行计算量分析时,不计入杂凑值的计算量。
在签名算法、签名验证算法两个步骤中,两种算法均使用了椭圆曲线上的运算和有限域上的模运算。对两种算法的总体运算量做具体统计分析,将有限域上的模加运算记为MA,将模逆运算记为MI,将模乘运算记为MM,将取模运算记为MO,将椭圆曲线上的倍点运算记为MP,将点加运算记为AP,得到SM2与ECDSA的数字签名计算量对比如表3所示。
表3 SM2与ECDSA的数字签名计算量对比
| 签名算法 | SM2 | ECDSA | |
|---|---|---|---|
| 签名产生 | 椭圆曲线运算 | 1MP | 1MP |
| 模运算 | 3MA+1MI+1MM | 1MA+1MI+1MM+1MO | |
| 签名验证 | 椭圆曲线运算 | 2MP+1AP | 2MP+1AP |
| 模运算 | 2MA | 2MA+1MI+1MO | |
由表3可知,不考虑杂凑值的计算量时,SM2数字签名算法的签名产生与签名验证计算量均与ECDSA相近。
2.1.3 数字签名算法性能测试分析
对SM2数字签名算法、ECDSA和RSA数字签名算法进行性能测试,循环次数N=1000。为保持安全强度的一致性,ECDSA算法的杂凑函数选用SHA-256。
1)去除杂凑算法对签名的影响
将杂凑算法运算耗时去除,对两种算法进行软件性能测试。将256 bit长度的随机数据模拟为由SM3和SHA-256产生的摘要值,作为SM2数字签名算法和ECDSA的输入,对该摘要数据进行签名及签名验证运算。
不计杂凑算法耗时在内的签名耗时比如表4所示,其中ECDSA_secp256k1表示ECDSA选取曲线secp256k1,此曲线为比特币所选择的曲线;ECDSA_X9.62prime256v1表示ECDSA选取曲线X9.62prime256v1,此曲线为EMV选择的NIST公布的曲线;SM2选取默认建议曲线。
表4 不计杂凑算法耗时在内的签名耗时比
| 算法 | 签名耗时比 | 签名验证耗时比 |
|---|---|---|
| ECDSA_secp256k1/OpenSSL SM2 | 1.11 | 1.12 |
| ECDSA_secp256k1/ECDSA_X9.62prime256v1 | 16.60 | 4.16 |
由表4可知,不计杂凑值耗时,在一般情况下(如ECDSA选取曲线secp256k1),OpenSSL SM2数字签名算法与ECDSA的签名和签名验证耗时相近,这与算法计算量分析结论相符。
此外,由于OpenSSL工具套件对X9.62prime256v1曲线做了算法层面的快速实现,使得ECDSA在选取此曲线时,数字签名性能得到大幅度提升。
2)杂凑算法对签名的影响
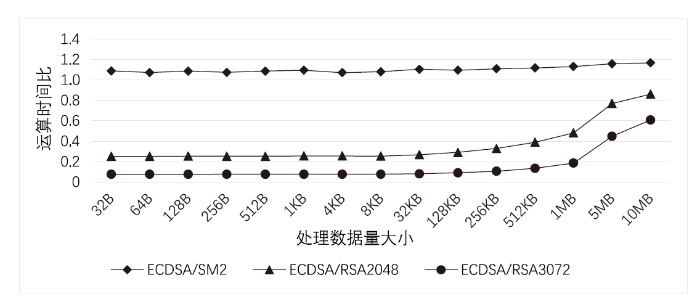
对不含杂凑运算的数字签名耗时测试能够验证算法的计算量理论分析结论,一个完整的数字签名过程包含对消息M的杂凑运算和对杂凑值数字签名运算两部分,杂凑运算会对签名算法的整体耗时产生影响。因此,对包含杂凑运算耗时在内的数字签名算法性能进行测试,在15组不同输入长度情况下,计算SM2数字签名算法、ECDSA(使用曲线secp256k1)、RSA算法的运行耗时比。其中,对RSA算法的2048 bit(当前各类系统中最常用的密钥长度,具有实际参考价值)和3072 bit(与SM2和ECDSA安全强度相当)密钥长度进行测试。3种数字签名算法的签名运算时间比如图2所示,3种数字签名算法的签名验证运算时间比如图3所示。
图2
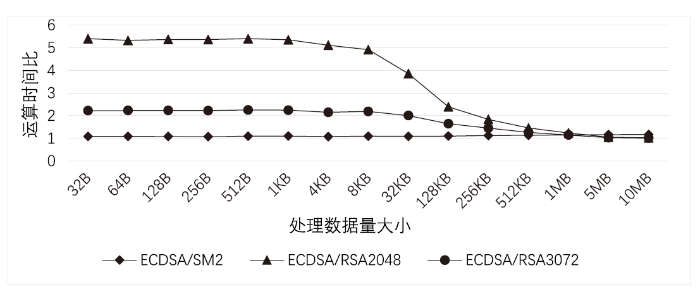
图3
此外,对于ECDSA和SM2数字签名算法,随着输入数据量的增多,最终两种算法签名和签名验证的效率比接近其所使用的杂凑函数效率比(杂凑函数效率比见1.3.1节)。当数据量较多时,杂凑函数的运算量在数字签名算法整体运算中占比很高,因此杂凑计算的开销成为算法的主要开销。
3)优化对算法性能的影响
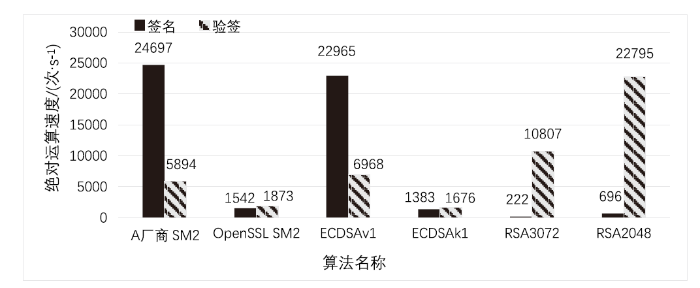
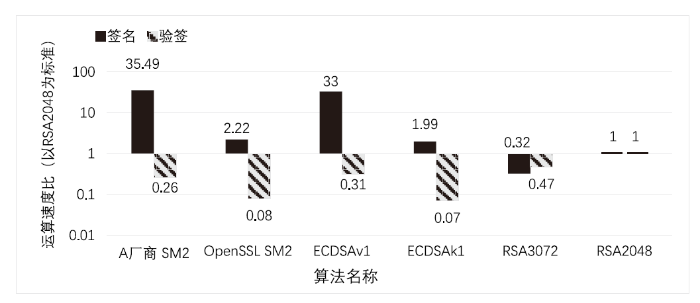
图4
图5
由上述测试结果分析可知,当不含杂凑运算开销时,SM2数字签名算法和ECDSA的性能相近;当杂凑运算包含在内时,随着数据量的增多,SM2数字签名算法和ECDSA的性能之比逐渐接近于SM3和SHA-256的性能之比。
在实际应用中,经过优化后的SM2性能得到了大幅度提升。从绝对数值方面来看,SM2中较慢的签名运算速度远高于RSA中较慢的签名运算速度,在同时需要使用签名和签名验证的场景中,优化后的SM2会更占优势。
2.2 公钥加密
公钥加密属于公钥算法的另一种应用,常用于加密重要数据。用户Y使用用户X的公钥对消息进行加密,用户X收到加密消息后使用自身的私钥对消息进行解密。本文将对SM2与ECIES、RSA算法应用于公钥加密的算法性能进行比较。
2.2.1 SM2、ECIES与RSA
SM2公钥加密算法与ECIES[9]算法均基于椭圆曲线密码体制进行加密,算法均由系统参数和辅助函数选取、加密算法、解密算法3个步骤组成。两种算法的整体结构相似,但算法细节存在区别。
整体而言,基于ECC的加密算法(ECIES与SM2公钥加密算法)与RSA算法的加密方法完全不同。前者是通过密钥派生函数KDF产生与加密数据m等长的密钥数据,并与明文异或后得到加密结果;后者加密需要先将明文分组、填充,再对各分组分别进行加密,对各分组加密结果进行拼接后得到最终加密结果。
2.2.2 公钥加密算法计算量
SM2公钥加密算法与ECIES算法的整体结构相似,最主要的区别是辅助函数的选取不同。SM2公钥加密算法指定唯一选取SM3,为保持安全强度的一致性,选用SHA-256/HMAC-SHA-256。
密钥派生函数KDF是辅助函数的重要组成部分,其原理是对输入数据进行多轮杂凑运算,得到特定长度的杂凑值为输出。SM2与ECIES的KDF设计区别在于输入数据内容和执行轮数均不同,前者的KDF函数输入数据长度长于后者,后者的执行轮数略大于前者。KDF函数不同的设计细节导致两种算法运算量的差别,具体表现为如下情况。
1)在数据量较少情况下,两种算法的KDF函数输入数据长度相差不大,每轮杂凑函数运算量也相差不大,由于ECIES执行轮数较多,因此SM2计算量小于ECIES。
2)在数据量较多情况下,KDF以及用于数据校验的杂凑运算成为加/解密计算的主要开销,此时大量的数据会造成SM2中每轮杂凑运算时处理的数据分组数大于ECIES,而执行轮数只是略少于ECIES。从整体来看,最终SM2计算量大于ECIES。
表5 SM2与ECIES的加/解密计算量对比
| 加/解密算法 | SM2 | ECIES | |
|---|---|---|---|
| 公钥加密 | 椭圆曲线运算 | 3MP | 2MP |
| 逻辑运算 | 1LO | 1LO | |
| 模乘运算 | — | 1MM | |
| 杂凑运算 | (klen/256)× HO1+1HO | ((klen+mackeylen)/256)HO2+1HH | |
| 私钥解密 | 椭圆曲线运算 | 2MP | 1MP |
| 逻辑运算 | 1LO | 1LO | |
| 模乘运算 | — | 1MM | |
| 杂凑运算 | (klen/256)HO | (klen/256)HO | |
由表5可知,SM2公钥加密算法的加密与解密计算量均与ECIES相近。由于KDF函数导致的计算量差异,在数据量较少时,SM2计算量略少于ECIES;在数据量较多时,SM2计算量会略多于ECIES。而RSA算法完全不同,无法直接进行理论推导,只能进行实际测试对比。
2.2.3 公钥加密算法性能测试分析
为了反映算法在实际使用中的性能表现,而ECIES在实际场景中使用较少,因此仅测试了SM2公钥加密算法(使用SM3)、OAEP填充模式(常用模式)下2048 bit与3072 bit RSA算法的耗时情况。测试结果中,以OpenSSL SM2算法为参考基准,不同输入长度下A厂商SM2、OpenSSL SM2与RSA加/解密的运行时间比如表6所示。
表6 不同输入长度下A厂商SM2、OpenSSL SM2与RSA加/解密的运行时间比
| 加/解密 | 输入长度 | A厂商SM2/ OpenSSL SM2 | RSA2048/ OpenSSL SM2 | RSA3072/ OpenSSL SM2 |
|---|---|---|---|---|
| 加密 | 16 B | 0.147787644 | 0.040161646 | 0.080578194 |
| 64 B | 0.148209251 | 0.039978619 | 0.080326983 | |
| 256 B | 0.151985583 | 0.079726359 | 0.080332399 | |
| 1 KB | 0.162721267 | 0.193082678 | 0.233398426 | |
| 4 KB | 0.201123432 | 0.688962323 | 0.837251662 | |
| 16 KB | 0.298521417 | 1.877450216 | 2.34507407 | |
| 32 KB | 0.364572911 | 2.688391462 | 3.371995372 | |
| 解密 | 16 B | 0.228408613 | 2.29651208 | 7.175291258 |
| 64 B | 0.226845092 | 2.263777384 | 7.07422817 | |
| 256 B | 0.234965591 | 4.537950334 | 7.082142906 | |
| 1 KB | 0.250163081 | 10.6395389 | 19.95441131 | |
| 4 KB | 0.301611021 | 35.33215849 | 65.68612578 | |
| 16 KB | 0.398097074 | 78.22104433 | 151.4175574 | |
| 32 KB | 0.446773723 | 100.6119596 | 196.0483998 |
由表6可知,整体来说,SM2公钥加密算法的加密与解密耗时接近,而RSA的加/解密耗时差别很大。随着数据量增多,RSA算法加/解密耗时明显增长,而SM2算法加/解密耗时增长较RSA而言较为平缓。
同时表6测试结果表明,在实际应用中,当数据量较少时,RSA加密耗时情况优于SM2算法;当数据量较多时,SM2算法的性能优于RSA,SM2解密相较于RSA具备明显优势。同时,通过对A厂商SM2与OpenSSL SM2的对比发现,该SM2算法在加/解密性能上都有了显著提升,分别达到OpenSSL SM2加/解密效率的6.8倍与4.4倍。并且该SM2算法相较于RSA在解密处理上具备了明显优势,解密运算效率在输入长度为16 B时已达到了RSA算法的10倍,且随着输入长度的增长,解密速度将远快于RSA。
3 分组算法
分组算法属于对称密码体制,其加密与解密密钥相同,主要用于大量数据的保密传输。
3.1 SM4、3DES和AES
表7 SM4、AES与3DES算法整体特性
| 算法 | 分组长度 /bit | 密钥长度 /bit | 迭代轮数 | 算法结构 | 算法特性 |
|---|---|---|---|---|---|
| SM4 | 128 | 128 | 32 | 非平衡Feistel网络 | 基本轮函数加迭代,含非线性变换 |
| AES | 128 | 128/182/ 256 | 10/12/14 | SP(代换- 置换)网络 | 排列、置换加迭代,含非线性变换 |
| 3DES | 64 | 112/168 | 16×3=48 | 平衡Feistel网络 | 使用标准的算术和逻辑运算,先替代后置换,不含非线性变换 |
3.2 分组算法计算量与安全性
在计算量方面,SM4与AES-128算法的计算量差别较大,因此不做计算量的统计与直接对比。在安全性方面,SM4的安全强度等同于AES-128,但是近年来一些密码分析表明,SM4的安全性略弱于AES-128[15]。由于SM4的密钥长度固定为128 bit,没有提供更长的可选密钥长度,在安全等级要求越来越高的情况下,SM4可能面临应用范围受限的问题。
3.3 分组算法性能测试分析
对SM4和AES算法进行性能测试,测试方法为对每轮数据循环迭代加密,循环次数N=10000,测试算法的加/解密运行速度。
1)算法性能对比
表8 ECB模式SM4与AES算法运行速度比
| 加/解密 | 输入长度 | A厂商SM4/AES | OpenSSL SM4/AES | AESEVP/AES |
|---|---|---|---|---|
| 加密 | 32 B | 0.99 | 0.81 | 10.69 |
| 128 B | 2.9 | 0.83 | 25.08 | |
| 512 B | 3.34 | 0.83 | 31.96 | |
| 1 KB | 3.35 | 0.84 | 33.54 | |
| 4 KB | 3.43 | 0.81 | 34 | |
| 16 KB | 3.54 | 0.82 | 35.1 | |
| 64 KB | 3.5 | 0.82 | 35.19 | |
| 256 KB | 3.53 | 0.82 | 35.4 | |
| 1 MB | 3.52 | 0.82 | 34.48 | |
| 解密 | 32 B | 1.31 | 1.07 | 11.13 |
| 128 B | 3.92 | 1.12 | 29.96 | |
| 512 B | 4.47 | 1.12 | 40.97 | |
| 1 KB | 4.47 | 1.12 | 43.08 | |
| 4 KB | 4.57 | 1.10 | 43.54 | |
| 16 KB | 4.71 | 1.11 | 45.04 | |
| 64 KB | 4.73 | 1.08 | 45.44 | |
| 256 KB | 4.74 | 1.13 | 45.7 | |
| 1 MB | 4.71 | 1.12 | 45.48 |
表9 CBC模式SM4与AES算法运行速度比
| 加/解密 | 输入长度 | A厂商SM4/AES | OpenSSL SM4/ AES | AESEVP/AES |
|---|---|---|---|---|
| 加密 | 32 B | 1.52 | 1.19 | 8.53 |
| 128 B | 1.18 | 0.89 | 6.55 | |
| 512 B | 1.09 | 0.82 | 6.02 | |
| 1 KB | 1.07 | 0.80 | 5.92 | |
| 4 KB | 1.05 | 0.80 | 5.93 | |
| 16 KB | 1.05 | 0.80 | 5.92 | |
| 64 KB | 1.05 | 0.81 | 5.95 | |
| 256 KB | 1.04 | 0.80 | 5.84 | |
| 1 MB | 1.05 | 0.80 | 5.95 | |
| 解密 | 32 B | 1.23 | 1.09 | 10.75 |
| 128 B | 3.67 | 1.10 | 28.65 | |
| 512 B | 4.36 | 1.11 | 44.58 | |
| 1 KB | 4.39 | 1.11 | 48.78 | |
| 4 KB | 4.56 | 1.11 | 52.46 | |
| 16 KB | 4.61 | 1.11 | 53.39 | |
| 64 KB | 4.63 | 1.11 | 53.93 | |
| 256 KB | 4.63 | 1.10 | 54 | |
| 1 MB | 4.66 | 1.11 | 54.05 |
由表8可知,ECB模式下AES加密性能高于OpenSSL SM4,解密性能OpenSSL SM4略高于AES。通过对比可以发现,A厂商优化后的SM4算法加/解密速度均优于标准AES软实现,约为标准AES软实现的3.5倍,为OpenSSL SM4的4倍,但与硬件AES-NI仍差距较大。
由表9可知,CBC模式下AES加密性能高于OpenSSL SM4,OpenSSL SM4解密性能略高于AES,整体效果无较大差异。通过对比可以发现,A厂商优化后的SM4算法加/解密速度均优于标准AES软实现,其中加密运算约为标准AES软实现的1.5倍,为OpenSSL SM4的1.3倍;解密运算约为标准AES软实现的4.6倍,为OpenSSL SM4的4.2倍,但加/解密均与硬件AES-NI的差距较大。
2)硬件加速对算法性能的影响
OpenSSL提供了EVP接口,此接口封装了多种密码算法,在实际使用时,通常会调用AES算法的EVP接口来实现加/解密运算。EVP接口支持调用AES-NI硬件加速技术,使算法性能大幅度提升。
由上述分析可知,SM4加/解密性能整体上与AES相差不大,在加密运算上性能稍差。经过A厂商优化后的SM4性能有显著提升,且明显优于AES软实现,但与硬件AES-NI仍存在较大差距。
4 优化建议
在类似于OpenSSL的各种软件库中,由于缺乏对应于国密算法的优化手段,使得国密算法性能较差。目前我国商用密码产业日益发展,已有超过2000款商用密码产品取得了国家密码管理局审批型号,其中软件实现的国密算法较少,已有的软件实现的国密算法性能指标也大多不理想,无法实现广泛应用。但也有一些优化效果较好的产品,从本文对我国A厂商优化后的国密算法性能测试数据来看,虽然与国际密码算法仍存在一定差距,但优化后的国密算法在部分场景中已经具备了一定优势,如SM2签名、SM2解密、SM4加/解密等。
为提升国密算法的性能水平,基于本文的测试与研究分析结果,给出如下建议。
1)建议商用产品的生产单位参考国际上广泛应用的开源软件库中使用的优化技术,对国密算法进行优化。以SM3为例,可参照OpenSSL对SHA-256的优化代码,实现SM3算法的性能提升。
2)建议科研机构开展对SM2算法推荐使用曲线的研究,研究发现其他便于快速计算的曲线,或研究针对SM2当前推荐曲线的快速软件实现方法,从而大幅度提升SM2的性能。
3)建议商用密码的制定与推广单位参考AES-NI技术,与国产芯片厂商开展SM4的硬件集成加速合作,推进SM4在安全传输层(Transport Layer Security,TLS)协议、金融行业等方向的应用。
5 结束语
本文分别对SM3、SM2、SM4算法及其对标的国际密码算法进行理论层面的分析,包括算法异同、计算量与安全性比较等,并结合理论研究结论,对基于OpenSSL的各种算法进行性能测试,同时引入了A厂商优化后的国密算法进行对比测试。结合理论分析与测试结果可知,SM3的性能略差于SHA-256,SM2数字签名算法与ECDSA算法的性能相近,SM2公钥加密算法与ECIES算法性能相差不明显,SM4的性能低于AES,高于3DES。
此外,由于针对国密算法的检测标准体系尚不健全,缺乏对国密算法性能及相应产品功能的评测标准,影响了国产商用密码的进一步发展。
随着国密SM系列算法逐步被纳入国际标准,越来越多地被集成于国际主流密码工具包中,国密算法的重要性越来越明显,对增强我国行业信息系统的“安全可控”能力意义重大。因此,增强对国密算法的软件性能优化,培养对全系列商用密码产品密码功能检测的能力,有助于推进国密算法标准的转化应用,为我国密码产业创造更加广阔的发展空间。
参考文献
Federal Information Processing Standards Publication 180-3, Secure Hash Standards(SHS)
[S].
How to Break MD5 and Other Hash Functions
SM3 Cryptographic Hash Algorithm
[EB/OL]. https://sca.gov.cn/sca/xwdt/2010-12/17/content_1002389.shtml,
SM3密码杂凑算法
[EB/OL]. https://sca.gov.cn/sca/xwdt/2010-12/17/content_1002389.shtml,
Analysis of SM3 Cryptographic Hash Algorithm
[D].
SM3密码杂凑算法分析
[D].
Public Key Cryptographic Algorithm SM2 Based Elliptic Curves
[EB/OL]. https://sca.gov.cn/sca/xwdt/2010-12/17/content_1002386.shtml,
SM2椭圆曲线公钥密码算法
[EB/OL]. https://sca.gov.cn/sca/xwdt/2010-12/17/content_1002386.shtml,
The Elliptic Curve Digital Signature Algorithm (ECDSA)
[J].DOI:10.1007/s102070100002 URL [本文引用: 1]
A Method for Obtaining Digital Signatures and Public-key Cryptosystems
[J].DOI:10.1145/357980.358017 URL [本文引用: 1]
The Comparision Between Digital Signature Based on SM2 and ECDSA
[J].
国密SM2数字签名算法与ECDSA算法对比分析研究
[J].
Public Key Cryptography for the Financial Services Industry, Key Agreement and Key Transport Using Elliptic Curve Cryptography
[J].DOI:10.1017/S0038713400003262 URL [本文引用: 1]
Data Encryption Standard(DES)
[J].
Rijndael, the Advanced Encryption Standard
[J].
Announcement of the State Password Administration(No.7)
[EB/OL]. https://www.oscca.gov.cn/sca/xwdt/2006-01/06/content_1002355.shtml, 2016-11-04.
国家密码管理局公告(第7号)
[EB/OL]. https://www.oscca.gov.cn/sca/xwdt/2006-01/06/content_1002355.shtml, 2016-11-04.
On the Security of Multiple Encryption
[J].DOI:10.1145/358699.358718 URL [本文引用: 1]
A Known-plaintext Attack on Two-key Triple Encryption
[J].
The Design of Rijndael
[J].